깃허브: https://github.com/PSLeon24/DataStructure/blob/main/Sorting%20algorithm.ipynb
셸 정렬(Shell Sort)
셸 정렬은 앞서 학습한 단순 삽입 정렬의 장점은 살리고 단점은 보완하여 더 빠르게 정렬하는 알고리즘
(단순 삽입 정렬 더보기: https://psleon.tistory.com/33)
단순 삽입 정렬의 문제
[1, 2, 3, 4, 5, 0, 6]
위와 같은 리스트가 있을 때 단순 삽입 정렬을 진행하면,
두 번째 원소인 2부터 3, 4, 5 순서대로 선택하며 정렬하는데 이 과정에서는 이미 정렬을 마친 상태이므로 원소의 이동(swap)이 발생하지 않아 아주 빠르게 완료됨
하지만 여섯 번째 원소인 0을 삽입 정렬하려면 아래와 같이 총 6번에 걸쳐 원소를 이동해야 함
1) [1, 2, 3, 4, 5, 0, 6]
2) [1, 2, 3, 4, 5, 5, 6]
3) [1, 2, 3, 4, 4, 5, 6]
4) [1, 2, 3, 3, 4, 5, 6]
5) [1, 2, 2, 3, 4, 5, 6]
6) [0, 1, 2, 3, 4, 5, 6]
1) ~ 5): 0보다 작은 원소를 만날 때까지 이웃한 왼쪽 원소를 하나씩 대입하는 작업을 반복
6): 멈춘 위치에 0을 대입
단순 삽입 정렬의 특징
| 장점 | 이미 정렬을 마쳤거나 정렬이 거의 끝나가는 상태에서는 속도가 아주 빠름 |
| 단점 | 삽입할 위치가 멀리 떨어져 있으면 이동 횟수가 많아짐 |
셸 정렬(Shell Sort)
셸 정렬은 이후 퀵 정렬이 고안되기 전까지는 가장 빠른 알고리즘으로 알려졌었음
셸 정렬은 먼저 정렬할 배열의 원소를 그룹으로 나눠 그룹별로 정렬을 수행함
그 후 정렬된 그룹을 합치는 작업을 반복해 원소의 이동 횟수를 줄임
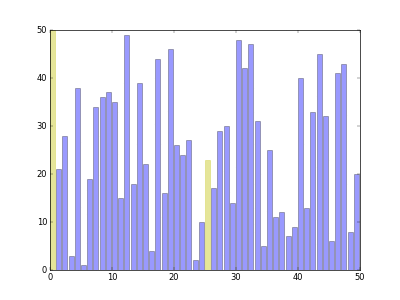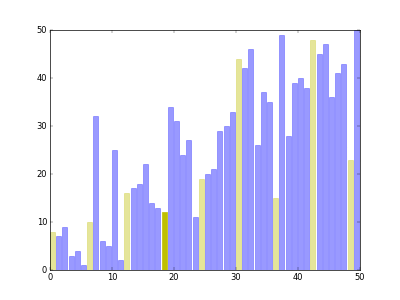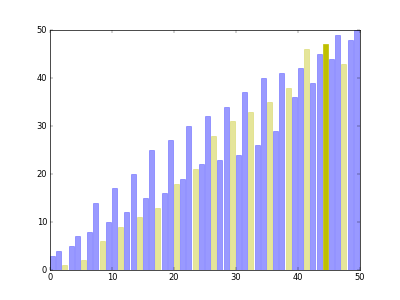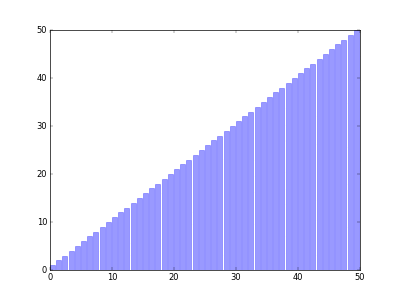
[8, 1, 4, 2, 7, 6, 3, 5]
위와 같은 리스트가 있을 때를 예를 들면,
1) 먼저 서로 4칸씩 떨어진 원소를 꺼내어 그룹으로 나누고 그룹별로 각각 정렬
- (8, 7), (1, 6), (4, 3), (2, 5)와 같이 4개의 그룹으로 나눔
- (7, 8), (1, 6), (3, 4), (2, 5)로 정렬
2) 이어서 2칸 떨어진 원소를 모두 꺼내 두 그룹으로 나누고 정렬을 수행
- (7, 8, 3, 4), (1, 6, 2, 5)와 같이 2개의 그룹으로 나눔
- (3, 4, 7, 8), (1, 2, 5, 6)으로 정렬
3) 점차 조금 더 정렬 된 상태에 가까워짐, 마지막으로 배열 전체를 묶어서 단순 삽입 정렬을 한 번 수행
- [1, 2, 3, 4, 5, 6, 7, 8]
위에서 한 것처럼 서로 4칸 떨어진 원소를 정렬하는 방법을 '4-정렬'이라 하고, 서로 2칸 떨어진 원소를 정렬하는 방법을 '1-정렬'이라 하며, 배열 전체에 적용하여 정렬하는 방법을 '1-정렬'이라 함
따라서 셸 정렬은 정렬 횟수는 늘어나지만 전체적으로 원소의 이동 횟수가 줄어들어 효율적
파이썬 실습

while문 안에 for문을 보면, 단순 삽입 정렬을 수행하는 과정으로 단순 삽입 정렬을 파이썬으로 구현한 코드와 거의 동일
(단순 삽입 정렬 더보기: https://psleon.tistory.com/33)
다만, 주목하는 원소와 비교하는 원소가 서로 이웃하지 않고 h개만큼 떨어져 있다는 것이 다름
while문 바로 윗줄에서 h를 전체 배열의 절반값으로 초기화 후, while문을 반복할 때마다 현재 h값에서 2로 나눈 값으로 업데이트함
h값의 선택
위의 경우 전체 배열의 크기는 9
따라서 h = 4 → 2 → 1와 같이 변화
h값은 n부터 감소하다가 마지막에는 1이 됨
추가로, h값을 어떠한 수열을 사용하면 간단하고 효율적인 정렬을 할 수 있음
'Algorithms & Data Structure' 카테고리의 다른 글
| [Algorithms] 문자열 검색(String Searching) (0) | 2023.05.17 |
|---|---|
| [Algorithms] 퀵 정렬(Quick Sort) (2) | 2023.05.09 |
| [Algorithms] 단순 삽입 정렬(Straight Insertion Sort) (0) | 2023.05.03 |
| [Algorithms] 버블 정렬(Bubble Sort) (0) | 2023.05.02 |
| [Algorithms] 단순 선택 정렬(Straight Selection Sort) (0) | 2023.05.02 |
