탐욕법(Greedy)
탐욕법(greedy): 그리디는 단순하지만 강력한 알고리즘이다. 탐욕법이라는 이름에서 알 수 있듯이 어떠한 문제가 있을 때 탐욕적으로 문제를 해결하는 알고리즘이다. 이때, '탐욕적'이라는 말은 '현재 상황에서 지금 당장 좋은 것만 고르는 방법'을 의미한다. 이러한 탐욕법 유형은 사전에 외우고 있지 않아도 풀 수 있을 가능성이 매우 높으며 문제를 풀기 위한 최소한의 창의력만 있으면 해결이 가능하다.
그리디 알고리즘은 기준에 따라서 최적의 방법을 선택하는 알고리즘이므로 '가장 큰 순서대로', '가장 작은 순서대로'와 같은 기준을 제시해준다. 대체로 이 기준은 정렬 알고리즘을 사용했을 때 만족시킬 수 있으므로 그리디와 정렬 알고리즘은 자주 짝을 이뤄 출제된다.
이제 기본적인 문제 유형을 알았으니 예제를 통해 문제를 살펴보자.
본 예제와 실전 문제는 '(나동빈) 이것이 코딩 테스트다 with 파이썬, p.87~p.102'의 내용이다.
예제1. 거스름돈
당신은 음식점의 계산을 도와주는 점원이다. 카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원짜리 동전이 무한히 존재한다고 가정한다. 손님에게 거슬러 줘야 할 돈이 N원일 때 거슬러줘야 할 동전의 최소 개수를 구하라. 단, 거슬러 줘야 할 돈 N은 항상 10의 배수이다.
위 문제는 그리디 알고리즘을 공부하면 항상 등장하는 대표적인 예제이다. 이 문제를 해결하기 위한 아이디어를 상식 수준에서 생각해보자.
거슬러줘야 할 동전이 최소 개수가 되기 위해서는 거스름돈으로 사용한 단위를 가장 큰 화폐 단위부터 거슬러 주면 된다.
예를 들어, 1300원을 거슬러 줘야한다고 생각해보자. 그렇다면 위 문제에서는 500원이 가장 큰 화폐 단위이므로 500원을 2개, 100원을 3개로 거슬러 주면 동전의 개수가 5개로 가장 최소가 된다.
어떻게 구했는지 식으로 작성해보면 N//500을 먼저 수행하고, (N%500)에 대해서 (N%500)//100을 수행했다. 그러면 나머지 50, 100도 이와 같은 방법으로 반복해서 식이 작성될 것이다. 이 해결 아이디어를 코드로 작성하면 아래와 같다.
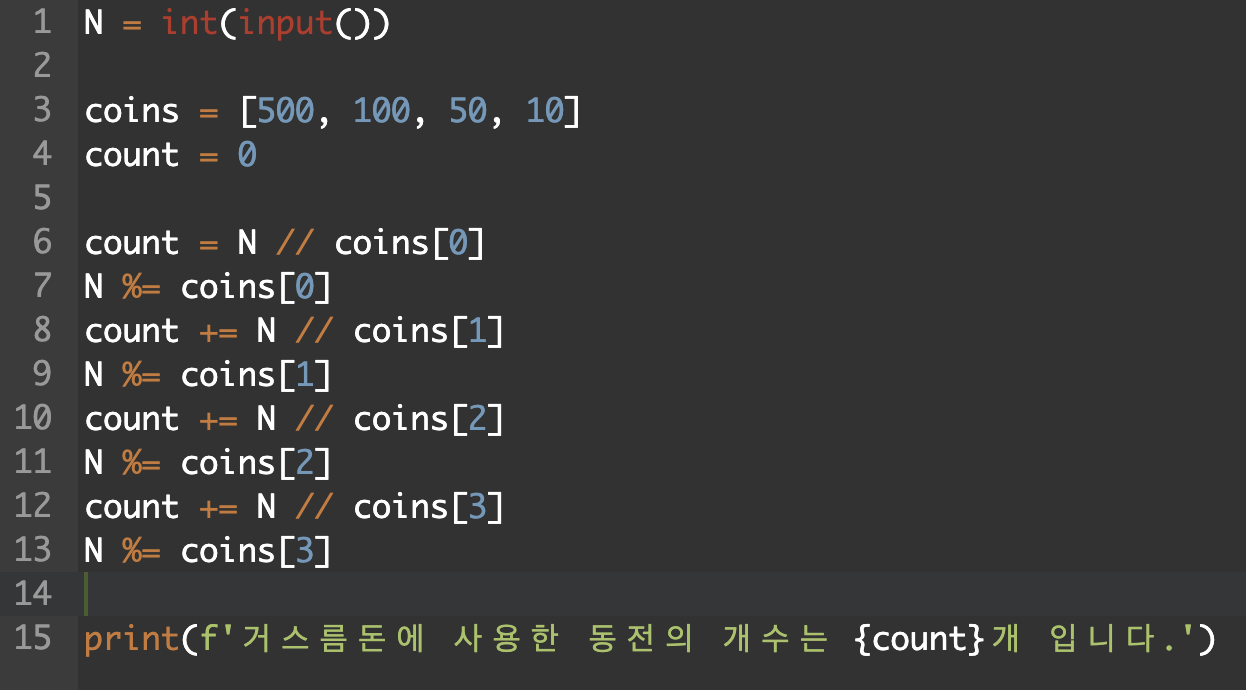

코드를 작성한 후 1300을 입력해보면 우리가 구했던 최소 개수인 5개가 출력된다.
그런데 코드를 보면 중복되는 부분이 너무 많다. 이런 중복된 구문은 for문이나 while문과 같이 반복문을 사용해서 간결하게 만들 수 있다.

위 코드를 작동시켜 보면, 똑같은 결과가 나오는데 코드는 훨씬 간결하고 가독성이 높아졌음을 확인할 수 있다.
이 예제는 그리디 알고리즘 중에서도 매우 쉬운 편에 속한다. 실제 코딩 테스트에서는 이보다 난이도가 높은 편이다. 하지만 거스름돈 예제와 문제에 접근하는 방법은 유사하므로 잘 기억해 두자.
자, 이제는 거스름돈 문제와 같은 유형의 문제를 무조건 그리디 알고리즘으로만 접근하는게 옳은 방법인지 고민해보자.
우리가 이 문제를 그리디 알고리즘으로 해결할 수 있었던 이유는 갖고 있는 동전 중에서 큰 단위가 항상 작은 단위의 배수이므로 작은 단위의 동전들을 종합해서는 다른 정답이 나올 수 없었기 때문이다. 하지만 800원을 거슬러 줘야 하는데, 거스름돈으로 사용할 동전의 단위가 500원, 400원, 100원이라고 생각해보자.
500원 1개, 100원 3개가 옳을까? 그렇지 않다. 그 이유는 400원 2개가 거스름돈에 사용한 최소 동전의 개수이기 때문이다.
이렇게 변형된 문제와 같이 거스름돈 문제에서 동전의 단위가 서로 배수 형태가 아닐 경우에는 그리디가 아닌 차후에 다룰 다이나믹 프로그래밍(DP)으로 해결할 수 있다.
대부분의 그리디 알고리즘 문제는 이처럼 문제 해결을 위한 최소한의 아이디어를 떠올리고 이것이 정당한지 검토할 수 있어야 답을 도출할 수 있다.
이제 그리디 알고리즘의 기본 원리에 대해 학습했고, 예제도 해결해 보았으니 실전 문제를 풀어보자.
실전 문제 - 큰 수의 법칙
난이도: 하 | 풀이 시간: 30분 | 시간 제한: 1초 | 메모리 제한: 128M | 기출: 2019 국가 교육기관 코딩테스트
'큰 수의 법칙'은 일반적으로 통계 분야에서 다루어지는 내용이지만 동빈이는 본인만의 방식으로 다르게 사용하고 있다. 동빈이의 큰 수의 법칙은 다양한 수로 이루어진 배열이 있을 때 주어진 수들을 M번 더하여 가장 큰 수를 만드는 법칙이다. 단, 배열의 특정한 인덱스(번호)에 해당하는 수가 연속해서 K번을 초과하여 더해질 수 없는 것이 이 법칙의 특징이다.
예를 들어 순서대로 2, 4, 5, 4, 6으로 이루어진 배열이 있을 때 M이 8이고, K가 3이라고 가정하자. 이 경우 특정한 인덱스의 수가 연속해서 세 번까지만 더해질 수 있으므로 큰 수의 법칙에 따른 결과는 6 + 6 + 6 + 5 + 6 + 6 + 6 + 5인 46이 된다.
단, 서로 다른 인덱스에 해당하는 수가 같은 경우에도 서로 다른 것으로 간주한다. 예를 들어 순서대로 3, 4, 3, 4, 3으로 이루어진 배열이 있을 때 M이 7이고, K가 2라고 가정하자. 이 경우 두 번째 원소에 해당하는 4와 네 번째 원소에 해당하는 4를 번갈아 두 번씩 더하는 것이 가능하다. 결과적으로 4 + 4 + 4 + 4 + 4 + 4 + 4인 28이 도출된다.
배열의 크기 N, 숫자가 더해지는 횟수 M, 그리고 K가 주어질 때 동빈이의 큰 수의 법칙에 따른 결과를 출력하시오.
입력 조건
- 첫째 줄에 N(2 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000)의 자연수가 주어지며, 각 자연수는 공백으로 구분한다.
- 둘째 줄에 N개의 자연수가 주어진다. 각 자연수는 공백으로 구분한다. 단, 각각의 자연수는 1 이상 10,000 이하의 수로 주어진다.
- 입력으로 주어지는 K는 항상 M보다 작거나 같다.
출력 조건
첫째 줄에 동빈이의 큰 수의 법칙에 따라 더해진 답을 출력한다.
입력 예시
5 8 3
2 4 5 4 6
출력 예시
46
이 문제를 정리하면 어떤 배열이 있을 때, 그 배열에서 주어진 수들 중에서 M번을 더해서 가장 큰 수를 만드는데 더할 때 한 숫자는 최대 K번 번까지만 더할 수 있다는 것이다.
해결 아이디어를 떠올리기 위해 문제에서 주어진 예를 다시 살펴보자.
'예를 들어 순서대로 2, 4, 5, 4, 6으로 이루어진 배열이 있을 때 M이 8이고, K가 3이라고 가정하자. 이 경우 특정한 인덱스의 수가 연속해서 세 번까지만 더해질 수 있으므로 큰 수의 법칙에 따른 결과는 6 + 6 + 6 + 5 + 6 + 6 + 6 + 5인 46이 된다.'
[2, 4, 5, 4, 6]이라는 배열에서 최댓값인 6을 K번인 3번 더하고, 6을 제외하고 살펴봤을 때의 최댓값인 5를 한 번 더하고 다시 6을 3번 더하고 그 다음 5를 더한다.
다른 예시를 살펴보자.
단, 서로 다른 인덱스에 해당하는 수가 같은 경우에도 서로 다른 것으로 간주한다. 예를 들어 순서대로 3, 4, 3, 4, 3으로 이루어진 배열이 있을 때 M이 7이고, K가 2라고 가정하자. 이 경우 두 번째 원소에 해당하는 4와 네 번째 원소에 해당하는 4를 번갈아 두 번씩 더하는 것이 가능하다. 결과적으로 4 + 4 + 4 + 4 + 4 + 4 + 4인 28이 도출된다.
만약에 최댓값이 동일한데 두 개 이상일 경우에는 서로 다른 것으로 간주하므로 최대값을 M번 곱해주면 해결된다.
위에서 생각해낸 문제 해결 아이디어를 코드로 작성하면 아래와 같다.



이 문제의 경우, M의 범위가 10,000 이하이므로 for문과 같이 반복문을 이용한 방식만으로도 시간 제한 1초 이내에 문제를 해결할 수 있다.
하지만 M의 크기가 100억 이상처럼 커진다면 시간 초과 판정을 받아 코드를 새로 작성해야 할 것이다. 이 문제를 간단한 수학적 아이디어를 이용해 해결해 보자.
예를 들어 N이 5이고, M이 8이고, K가 3이고 배열이 [2, 4, 5, 4, 6]으로 주어졌다고 가정하자.
이때 가장 큰 수는 6이고 두 번째로 큰 수는 5이다.
이 경우 큰 수의 법칙으로 만들 수 있는 가장 큰 수는 6 + 6 + 6 + 5 + 6 + 6 + 6 + 5 = 46이다.
이때, 6 + 6 + 6 + 5가 반복된다는 것을 파악하는 것이 중요하다. 즉, 가장 큰 수와 두 번째로 큰 수가 더해질 때는 특정한 수열 형태로 일정하게 반복해서 더해지는 특징이 있다.
그렇다면 이렇게 반복되는 길이는 어떻게 구할 수 있을까? 생각해보면 가장 큰 수를 K번 더하고 그 다음으로 큰 수를 한번만 더하기 때문에 K + 1이 된다. 따라서 M을 (K + 1)로 나눈 몫이 이 수열이 반복되는 횟수가 된다. 위 예시에서는 8을 4로 나눈 몫이 2이므로 6 + 6 + 6 + 5가 총 두 번 반복된다는 것을 알 수 있다. 여기서 이제 K를 곱해주면 가장 큰 수가 등장하는 횟수가 된다.
이때 M이 (K + 1)로 나누어떨어지지 않는 경우도 고려해야 한다. 그럴 때는 M을 (K + 1)로 나눈 나머지만큼 가장 큰 수가 추가로 더해지므로 이를 고려해주어야 한다.
즉, 가장 큰 수가 더해지는 횟수'는 다음과 같다.
int(m / (k + 1)) * k + m % (k + 1)
이를 토대로 코드를 작성하면 아래와 같이 불필요한 연산을 줄여 효율적으로 개선했음을 확인할 수 있다.

'Algorithms & Data Structure' 카테고리의 다른 글
| [Algorithms] 그리디 - 1이 될 때까지 (0) | 2023.07.13 |
|---|---|
| [Algorithms] 그리디 - 숫자 카드 게임 (0) | 2023.07.13 |
| [Algorithms] 셰이커 정렬(Shaker Sort) (0) | 2023.05.30 |
| [Data Structure] 원형 이중 연결 리스트(Circular Doubly Linked List) (0) | 2023.05.30 |
| [Algorithms] 4퀸 문제 및 8퀸 문제 (4-Queen problem & 8-Queen problem) (0) | 2023.05.23 |
