[AI] Activation function - Sigmoid function | 활성화 함수 - 시그모이드 함수

Activation function - Sigmoid function

활성화 함수(Activation function)

→ 더보기: https://psleon.tistory.com/19

입력 신호의 총합을 출력 신호로 변환하는 함수 ← 입력 데이터를 다음 레이어로 어떻게 출력하느냐를 결정하는 역할이기 때문에 매우 중요

 

이전에 공부한 퍼셉트론의 경우 활성화 함수로 계단 함수를 사용하지만, 제대로 된 신경망을 구현하기 위해서는 다양한 활성화 함수가 필요

대표적인 활성화 함수로는 Sigmoid, ReLU(가장 많이 사용) 등이 있는데, 본 포스팅에서는 시그모이드부터 정복하고자 함

 

시그모이드 함수(Sigmoid function)

시그모이드 함수는 다른 말로 로지스틱 함수(logistic function)라고도 하며, 입력받는 x의 값에 따라 0~1의 값을 출력하는 S자 형태의 함수이고 실제 모양이 S자 형태를 띄기 때문에 시그모이드라는 이름이 붙여졌다고 한다.

정의

sigmoid function definition

주피터 노트북으로 실습

Sigmoid function

 

시그모이드 함수의 도함수

derivative of sigmoid

derivative of sigmoid function

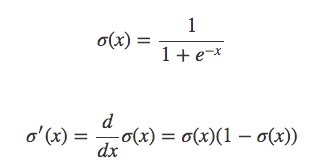
그래프의 미분계수를 보면 최댓값은 0.25임을 확인할 수 있음

딥러닝에서 학습을 위하여 역전파를 계산하는 과정에서 활성화 함수의 미분 값을 곱하는 과정이 포함됨

sigmoid function

이때, 시그모이드를 활성화 함수로 사용하는 경우 은닉층의 깊이가 깊다면 오차율 계산이 어렵다는 문제 발생하여 기울기 소멸 문제(Vanishing Gradient Problem)가 발생함

시그모이드 함수는 입력값이 크거나 작을 때 출력값이 기울기가 매우 작아져서 0에 가까워지는 경향이 있어 이럴 경우, 미분 값이 소실될 가능성이 있는데 이를 '기울기 소멸'이라고 함

→ 즉, x의 절대값이 커질수록(도함수 그래프 참고) Gradient Backpropagation시 미분 값이 소실될 가능성이 있음

Backpropagation: https://thehackweekly.com/8-most-popular-types-of-activation-functions-in-neural-networks/

Gradient Backpropagation를 하게 되면 output부터 반대로 미분값을 계속해서 곱해서 계산하게 되는데, 이때 은닉층의 깊이가 깊다면 시그모이드의 도함수의 최댓값인 0.25 이하의 값을 계속 곱하게 되는데 1보다 작은 수를 무수히 많이 곱하다 보면 0에 가까워짐.

만약 기울기가 거의 0으로 소멸되어 버리면 학습은 매우 느려지고, 학습이 다 이루어지지 않은 상태에서 멈출 것 → '지역 최솟값에 도달한다'고 표현함

끝에서부터 점점 back propagation에서 깊숙히 들어갈수록 1보다 작은 값들이 계속 곱해지므로 기울기가 거의 0으로 수렴하게 됨

이러한 문제점을 해결하기 위해서는 ReLU와 같은 비선형 함수를 사용하면 됨(사라져가는 성질을 갖고 있지 않으므로)

ReLU Activation Function

 

또한 Sigmoid 함수의 중심이 0이 아니기 때문에 학습이 느려질 수 있는 단점이 있음

→ 한 노드에서 모든 파라미터의 미분 값은 모두 같은 부호를 같게 되는데, 같은 방향으로 update되는 과정은 학습을 지그재그 형태로 만드는 원인을 낳음