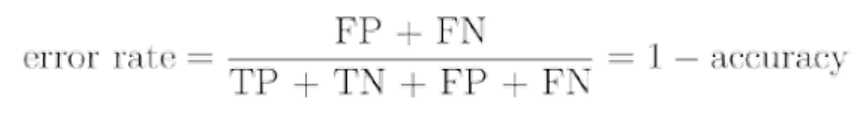반응형
Yeongmin Ko's learning notes
- Classification: KNN, Decision Tree
- Regression: Linear and Logistic Regression
- Clustering: K-Means, Agglomerative Clustering, DBSCAN

- 군집화(Clustering): 서로 유사한 데이터 개체 집합을 하위 집합으로 분할하는 프로세스(The process of partitioning a set of data objects that are similar to each other into subsets)

- 이때, 각 하위 집합을 클러스터라고 부름(A subset is called cluster)

- K-Means(K-평균)
- K는 클러스터(하위 집합)의 갯수(K is number of clusters)
- 중심 기반 테크닉(A centroid-based technique)
- Centroid는 각 클러스터에 속한 객체의 평균(Centroid is the average of objects belonging to each cluster)
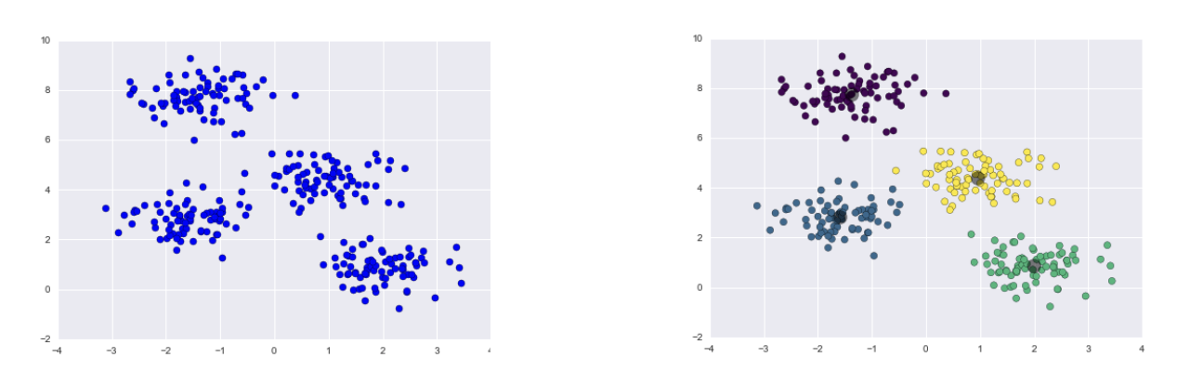
- 위 그림의 경우, K = 4
- 작동 알고리즘
- Step 1. 군집의 갯수 k 결정(Determine parameter k (k > 0))
- Step 2. 초기 중심점 설정을 위해 k개의 점을 무작위로 선택
- Step 3. 모든 점을 가장 가까운 중심에 할당하여 k개의 클러스터를 형성
- Step 4. 각 클러스터의 중심점을 다시 계산(각 클러스터의 평균 계산)
- Step 5. 중심이 변하지 않을 때까지 3~4단계를 반복
- Agglomerative Clustering(병합 군집)
- 상향식 전략(Bottom-up strategy)
- 각 개체가 자체 클러스터를 형성하도록 하는 것부터 시작하여 모든 객체가 단일 클러스터에 포함될 때까지 클러스터를 점점 더 큰 클러스터로 반복적으로 병합
- 작동 알고리즘
- Step 1. 각 객체는 하나의 클러스터를 형성
- Step 2. 가장 낮은 수준에서 가장 가까운 두 개의 클러스터를 하나의 클러스터로 병합
- Step 3. 단일 클러스터가 될 때까지 2단계를 반복
- DBSCAN(밀도 기반 클러스터링)
- 어느 점을 기준으로 반경 radius 내에 점이 n개 이상 있으면 하나의 군집으로 인식하는 방식
- 점 p가 있을 때, 점 p에서 부터 거리 e(epsilon)내에 점이 m(minPts)개 있으면 하나의 군집으로 인식

- 어느 점을 기준으로 반경 radius 내에 점이 n개 이상 있으면 하나의 군집으로 인식하는 방식
- K 최근접 이웃(K-Nearest Neighbors)
- 새로운 데이터가 들어왔을 때 기존 데이터 중 새로운 데이터와 비슷한 속성의 그룹으로 분류하는 알고리즘(Classifies unlabeled data points by assigning them the class of similar labeled data points)
- 작동 알고리즘
- Step 1. 주변의 몇 개의 데이터와 비교할지 파라미터 k 결정(Determine parameter k (k > 0))
- Step 2. 새 데이터와 기존 데이터 간의 거리를 계산해서 두 데이터 간의 유사도 구하기(Determine similarity by calculating the distance between a test point and all other points in the dataset)
- Step 3. 2단계에서 계산한 거리 값에 따라 데이터 세트를 정렬(Sort the dataset according to the distance values)
- Step 4. k번째 최근접 이웃의 범주를 결정(Determine the category of the k-th nearest neighbors)
- Step 5. 새로운 데이터에 대해 k개의 최근접 이웃의 단순 다수결을 통해 범주를 결정(Use simple majority of the category of the k nearest neighbors as the category of a test point)
- 장점(advantages)
- 간단하고 상대적으로 효과적(Simple and relatively effective)
- 단점(disadvantages)
- Requires selection of an appropriate k
- k가 너무 작으면 모델이 복잡해서 과적합(overfitting)이 발생
- k가 너무 크면 모델이 너무 단순해져서 과소적합(underfitting)이 발생
- Does not produce a model
- 별도의 학습 모델을 생성하지 않기 때문에 새로운 데이터에 대해 매번 계산이 필요하므로 계산 비용이 높음
- Nominal feature and missing data require additional processing
- KNN은 주로 수치형 데이터에 사용되기 때문에 명목형 변수에 대해서는 라벨 인코딩이나 원핫 인코딩과 같은 방식으로 수치형으로 변환해야 하며 결측값의 경우 별도의 방식으로 전처리해야 하는 추가 비용이 발생
- Requires selection of an appropriate k
- 베이즈 정리(Bayes' theorem): 사전확률과 사후확률의 관계에 대해서 설명하는 정리


- 용어 정리
- 가설(H, Hypothesis): 가설 혹은 어떤 사건이 발생했다는 주장
- 증거(E, Evidence): 새로운 정보
- 우도(가능도, likelihood) = P(E|H): 가설(H)이 주어졌을 때 증거(E)가 관찰될 가능성
- 확률 vs 우도
- 확률: 특정 경우에 대한 상대적 비율
- 모든 경우에 대하여 더하면 1이 됨(Mutually exclusive & exhaustive)
- 우도: '가설'에 대한 상대적 비율
- 가설은 얼마든지 세울 수 있고, 심지어 서로간에 포함관계가 될 수도 있음(Not mutually exclusive & Not exhaustive)
- 확률: 특정 경우에 대한 상대적 비율
- 확률 vs 우도
- 사전확률(Prior probaility) = P(H): 어떤 사건이 발생했다는 주장의 신뢰도
- 사후확률(Posterior probability) = P(H|E): 새로운 정보를 받은 후 갱신된 신뢰도
- 작동 알고리즘
- Step 1. 주어진 클래스 라벨에 대한 사전 확률(Prior probability)을 계산
- Step 2. 각 클래스의 각 속성으로 우도 확률(Likelihood probability) 계산
- Step 3. 이 값을 Bayes Formula에 대입하고 사후 확률(Posterior probability)을 계산
- Step 4. 1~3의 결과로 어떤 클래스가 높은 사후 확률을 갖게 될 지 알 수 있음(입력 값이 어떤 클래스에 더 높은 확률로 속할 수 있을지)
- 연관 규칙(Association Rule)
- 데이터에서 변수 간의 유의미한 규칙을 발견하는 데 쓰이는 알고리즘
- e.g., 라면을 구매하는 고객이 햇반을 함께 구매할 가능성이 높다.
- 연관성 규칙 생성 과정
- Step 1. 지지도(Support, 교사건)
- 데이터에서 항목 집합이 얼마나 빈번하게 등장하는지를 나타내는 척도
- Support(X) = Count(X) / n
- Step 2. 신뢰도(Confidence, 조건부 확률)
- 조건부 아이템(A)을 구매한 경우, 이중에서 얼마나 결론부 아이템(B)을 구매할 것인지를 나타내는 척도
- Confidence(A → B) = Support(X, Y) / Support(X) = Support(X, Y) / Support(X)
- Step 1. 지지도(Support, 교사건)
- Apriori Algorithm
- 연관 규칙(association rule)의 대표적인 알고리즘으로, 특정 사건이 발생했을 때 함께 발생하는 또 다른 사건의 규칙을 찾는 알고리즘
- 작동 알고리즘
- Step 1. 모든 항목의 빈도를 계산하여 최소 지지도(minimum support)를 넘는 항목들만 남김
- Step 2. 남은 항목들을 조합하여 2개의 항목 집합으로 이루어진 후보 항목 집합을 만듦
- Step 3. 2단계에서 만든 후보 항목 집합으로부터 빈도를 계산하여 최소 지지도를 넘는 항목들만 남김
- Step 4. 후보 항목 집합이 더이상 나오지 않을 때까지 남은 항목들로부터 2~3단계를 반복 수행
- Step 5. 각 빈발 항목 집합에 대해 모든 가능한 연관 규칙을 생성하고 각각의 신뢰도(confidence)를 계산함
- Step 6. 신뢰도가 최소 신뢰도(minimum confidence)를 넘는 규칙들만 남김
- 협업 필터링(Collaborative Filtering)
- 제품 및 사용자 간의 유사성을 검토하고 이를 바탕으로 사용자 취향에 맞는 제품을 추천해주는 방식으로 사용자 기반 협업 필터링과 아이템 기반 협업 필터링으로 분류할 수 있음
- e.g., 특정 사용자와 비슷한 취향을 가진 사람이 좋아하는 음악은 특정 사용자도 좋아할 가능성이 높음
- 제품 및 사용자 간의 유사성을 검토하고 이를 바탕으로 사용자 취향에 맞는 제품을 추천해주는 방식으로 사용자 기반 협업 필터링과 아이템 기반 협업 필터링으로 분류할 수 있음
- Recommendation Systems Applications
AmazonNetflixWatcha
- 사용자 기반 협업 필터링(User-based filtering)
- Basic idea: 타겟 사용자와 관심사가 같은 유사 사용자 찾기
- e.g., 영화 추천 시스템에서 한 사용자가 특정 영화에 높은 평점을 줬다면, 이와 비슷한 취향을 가진 사용자들에게도 해당 영화를 추천

- 사용자 간의 유사성 계산(피어슨 상관계수 활용)


- 사용자 A와 B의 공분산을 각각의 표준편차의 곱으로 나누면 피어슨 상관계수를 구할 수 있음
- Basic idea: 타겟 사용자와 관심사가 같은 유사 사용자 찾기
- 아이템 기반 협업 필터링(Item-based filtering)
- Basic idea: 아이템 간의 유사성을 사용하여 추천 제공
- e.g., 대다수의 사용자가 A 영화에 이어 B 영화를 높게 평가했다면, A 영화를 선호하는 사용자에게 B 영화를 추천할 수 있음

- Basic idea: 아이템 간의 유사성을 사용하여 추천 제공
- 사용자 기반 협업 필터링의 장·단점
- 장점
- 직관성: 동일한 취향을 가진 사용자의 행동을 기반으로 추천을 제공하기 때문에 이해하기 쉬움
- 개인화된 추천: 비슷한 사용자를 찾음으로써 개인화된 추천이 가능함
- 신규 아이템 추천 가능: 새로운 아이템이 시스템에 추가되면 기존의 사용자 취향에 맞추어 쉽게 추천 가능
- 단점
- 확장성 문제: 사용자 수가 많아질수록 유사도 계산이 비효율적이게 됩니다. 특히 대규모 데이터셋에서는 계산 비용이 높음
- 희소성 문제: 사용자-아이템 매트릭스가 희소할 경우(많은 빈칸이 있는 경우) 유사한 사용자를 찾기가 어려움
- 콜드 스타트 문제: 새로운 사용자에 대해 충분한 정보가 없을 경우 추천이 어려움
- 장점
- 아이템 기반 협업 필터링의 장·단점
- 장점
- 확장성: 아이템 수는 일반적으로 사용자 수보다 적기 때문에 유사도 계산이 더 효율적
- 안정성: 아이템의 유사도는 시간에 따라 크게 변하지 않으므로 더 안정적인 추천이 가능함
- 희소성 문제 해결: 사용자가 적어도 하나의 아이템을 평가했다면 추천이 가능함
- 단점
- 신규 아이템 문제: 새로운 아이템에 대한 유사도 정보를 얻기 어려워 추천이 힘들 수 있음
- 개인화 부족: 사용자 기반 협업 필터링에 비해 개인화가 어려움. 특정 사용자의 취향보다는 아이템의 전반적인 유사성에 의존하기 때문
- 초기 학습 비용: 초기 아이템 간 유사도 계산에 많은 시간이 소요될 수 있음
- 장점
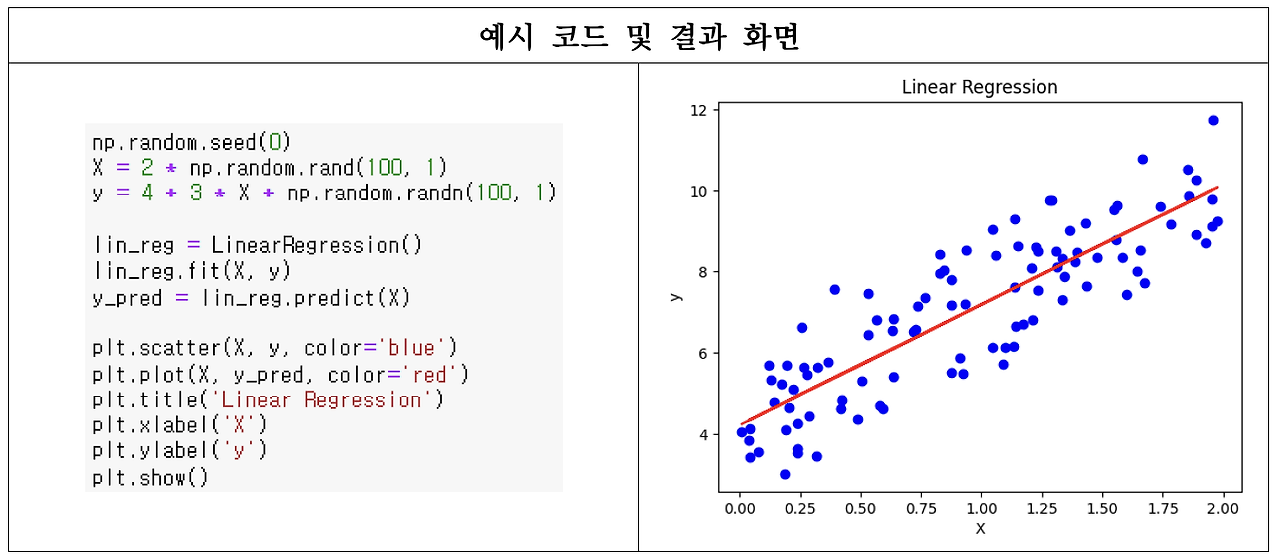
- 선형 회귀(Linear Regression): 주어진 데이터에서 독립 변수(X)와 종속 변수(Y) 간의 선형 관계를 모델링하여 연속적인 값을 예측하는 머신러닝 알고리즘(머신러닝 알고리즘이지만 인공신경망 알고리즘의 기초가 됨)

- 위 수식에서 𝛽는 회귀 계수, ϵ은 오차항이며, 회귀 계수를 찾기 위해 최소제곱법을 사용하여 오차 제곱합을 최소화
- 퍼셉트론(Perceptron): 퍼셉트론은 단층 신경망의 가장 기본적인 형태로, 선형 회귀와 유사한 구조를 가지며 이진 분류 문제를 해결하기 위해 사용
- 퍼셉트론은 입력값에 가중치를 곱한 후, 그 합을 활성화 함수(주로 계단 함수)를 통해 이진 출력을 생성

- 위 수식에서 step은 가중치 합을 입력으로 받아서 최종 출력을 결정하는 계단 함수이고, w는 가중치 벡터, 𝑥는 입력 벡터, 𝑏는 바이어스
- 계단 함수(step)의 수식:
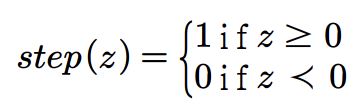

- 아달린(Adaline): 퍼셉트론과 유사하지만, 출력에 활성화 함수(계단 함수)를 적용하지 않고 선형 함수의 결과를 학습에 사용하는 것이 특징

- 위 수식에서 w는 가중치 벡터, 𝑥는 입력 벡터, 𝑏는 바이어스, 아데린은 평균 제곱 오차 함수를 사용하여 가중치를 업데이트하며, 연속적인 오차를 최소화

- 로지스틱 회귀(Logistic Regression): 이진 분류 문제를 해결하기 위해 고안된 방법으로, 입력 변수들의 선형 결합을 구한 후 이를 로짓 함수(또는 로지스틱 함수)를 통과시켜 확률을 예측
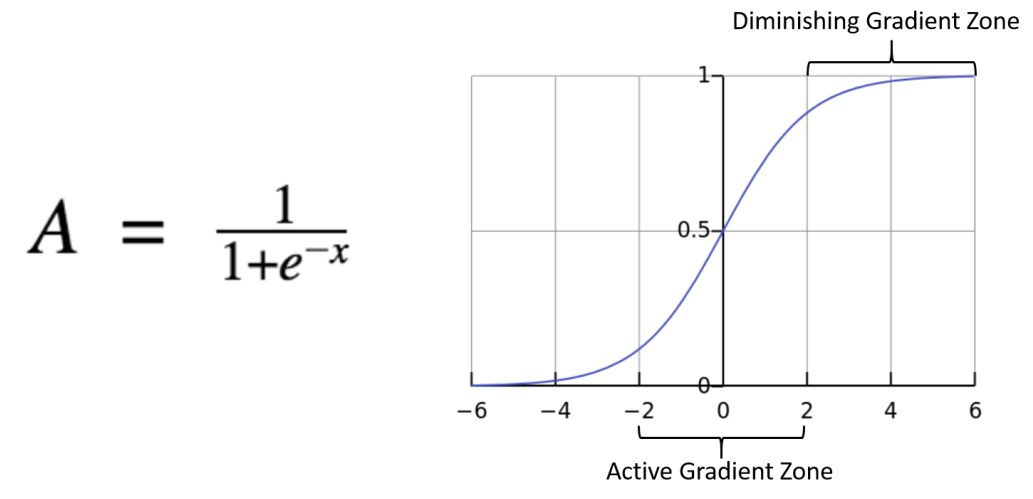
- 로짓 함수는 S자 형태를 띠며 0과 1 사이의 값을 가짐. 이 함수를 통과한 결과는 특정 사건이 발생할 확률로 해석되며, 이진 분류에서는 양성 클래스에 속할 확률로 해석
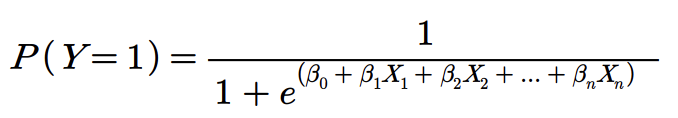
- 위 수식에서 𝑃(Y=1)은 양성 클래스에 속할 확률을 의미하며, X는 입력 변수, 𝛽는 회귀 계수를 나타냄. 모델은 주어진 데이터에서 확률을 최대화하는 회귀 계수를 찾기 위해 최대 우도 추정(MLE)법을 사용
- Odds(오즈): 성공 확률과 실패 확률의 비율 → 특정 사건이 발생할 확률을 그 사건이 발생하지 않을 확률과 비교한 값
- 0부터 1까지 증가할 때 오즈 비의 값은 처음에는 천천히 증가하다가 p가 1에 가까워지면 급격히 증가함
- Odds Ratio(오즈 비): p / (1 - p) (p = 성공 확률)
- e.g., 어떤 사건이 발생할 확률이 80%일 때의 odds ratio는?
- 0.8 / (1 - 0.8) = 0.8 / 0.2 = 4
- e.g., 어떤 사건이 발생할 확률이 80%일 때의 odds ratio는?
- Logit function(로짓 함수): 오즈의 자연 로그를 취한 값
- logit(p) = log(p / (1 - p))

- p가 0.5일 때 0이 되고 가 0과 1일 때 각각 무한대로 음수와 양수가 되는 특징을 가짐

- 활성화 함수: 선형 함수를 통과시켜 얻은 값을 임계 함수에 보내기 전에 변형시키는데 필요한 함수로, 주로 비선형 함수를 사용
- Why does Activation function use nonlinear function?
- 선형 함수(단순한 규칙)의 경우 직선으로 data를 구분하는데, 이는 아무리 층을 깊게 쌓아도 하나의 직선으로 규칙이 표현된다는 것을 뜻함. 즉, 선형 변환을 계속 반복하더라도 결국 선형 함수이므로 별 의미가 없음.
- 그러나, 비선형 함수의 경우 여러 데이터의 복잡한 패턴을 학습할 수 있고, 계속 비선형을 유지하기 때문에 다층 구조의 유효성을 충족시킬 수 있음. 또한, 비선형 함수는 대부분 미분이 가능하기 때문에 활성화 함수로 적합함.
- Why does Activation function use nonlinear function?
- Sigmoid function(시그모이드 함수)
- 단일층 신경망: 입력층과 출력층으로 구성된 가장 간단한 형태의 신경망. 주로 퍼셉트론, 아데린, 로지스틱 회귀와 같은 모델들을 포함할 수 있으며, 다양한 활성화 함수를 사용할 수 있어 비선형 문제를 해결할 수 있음

- 위 수식에서 f는 활성화 함수(예: 시그모이드 함수, ReLU 등), w는 가중치 벡터, 𝑥는 입력 벡터, 𝑏는 바이어스

- 피어슨 상관계수(Pearson Correlation): -1 ~ 1 사이의 가능한 유사도(Possible similarity values between -1 and 1)

- 1에 가까울 수록 양의 상관관계
- -1에 가까울 수록 음의 상관관계
- 0에 가까울 수록 상관관계 없음
- 코사인 유사도: 벡터 간의 각도를 측정해서 유사도 계산
- 내적 공식: A·B = ||A|| * ||B|| * cosθ
- 위 공식을 통해 cosθ = A·B / (||A|| * ||B||) 를 구할 수 있음
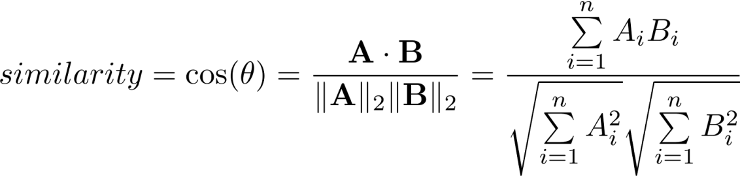
- Adjusted Rand Index
- 혼동행렬(Confusion matrix)
- 혼동행렬: 예측값이 실제값과 일치하는지 여부에 따라 분류한 표(a table that categorizes predictions according to whether they match the actual value)
- The most common performance measures consider the model's ability to discern one class versus all others
- The class of interest is known as the positive
- All others are known as negative
- The relationship between the positive class and negative class predictions can be depicted as a 2 x 2 confusion matrix
- True Positive(TP): Correctly classfied as the class of interest
- True Negative(TN): Correctly classified as not the class of interest
- False Positive(FP): Incorrectly classified as the class of interest
- False Negative(FN): Incorrectly classified as not the class of interest

- T와 F의 경우, True(참)와 False(거짓)을 나타내며, 예측값과 실제값이 일치하는 경우 T가 오고 예측값과 실제값이 다른 경우 F가 옴
- P와 N의 경우, Positive(긍정)와 Negative(부정)을 나타내며, 예측값이 양성 클래스(1)을 나타내는 경우 P가 오고 예측값이 음성 클래스(0)을 나타내는 경우 N이 옴
- e.g., 예측값=0, 실제값=0인 경우, TN
- e.g., 예측값=1, 실제값=0인 경우, FP
- 정확도(Accuracy): 2 x 2 혼동행렬에서, 아래와 같이 정확도를 수식화할 수 있음
- 오분류율(Error rate): 오분류율은 1에서 정확도를 빼면 됨
- 정밀도(Precision): 정밀도는 모델의 예측값이 긍정인 것들 중 실제값이 긍정인 비율을 나타냄

- 정밀도는 재현율과 헷갈리기 쉬운데, 예측값이 긍정이라는 키워드를 기억하면 분모의 수식인 TP + FP를 기억하기 쉬움
- 재현율(Recall): 재현율은 실제값이 긍정인 것들 중 예측값이 긍정인 비율을 나타냄

- 재현율은 정밀도와 헷갈리기 쉬운데, 실제값이 긍정이라는 키워드를 기억하면 분모의 수식인 TP + FN을 기억하기 쉬움
- F 점수(F-Score): 정밀도와 재현율의 조화평균
- 평균 제곱 오차(Mean Squared Error, MSE)
- 평균 절대 오차(Mean absolute error, MAE)
'AI & BigData' 카테고리의 다른 글
| AI 연구자가 말하는 ChatGPT 시대의 공부법 (1) | 2025.03.28 |
|---|---|
| Transformer (0) | 2024.07.22 |
| ADSP 3시간 공부 합격 후기 (0) | 2024.06.01 |
| [파이토치] 메타코드M '딥러닝 입문 + Pytorch 실습 부트캠프' 강의 후기(1/8) (1) | 2024.04.21 |
| [AI] 인공지능 대학원 면담 전공 및 수학(선형대수, 통계) 질문 및 답변 준비 (0) | 2024.04.11 |