이산확률분포 - 베르누이 분포, 이항분포(Bernoulli Distribution, Binomial Distribution)
이번 포스팅에서는 이산확률분포 중에서 베르누이 분포와 이항분포를 알아보고자 한다.
먼저, 이산확률분포가 무엇인지에 대한 개념을 정립하고 시작하자.
확률분포는 크게 2가지 카테고리로 분류할 수 있는데, 첫째는 이산확률분포(discrete probability distribution)이고 둘째는 연속확률분포(continuous probability distribution)이다. 이 둘의 차이를 가장 잘 나타내는 그림은 다음과 같다.

먼저, 이산확률분포는 가능한 결과가 특정한 유한 또는 계산할 수 있는 무한집합을 가지는 확률분포로써 주로 정수값을 가진다. 쉽게 말하면, 특정 범위 내에서 정확한 값으로만 가질 수 있는 확률분포인 것이다. 예를 들면, 주사위를 던졌을 때 나오는 값과 같은 경우는 1~6까지 이산적인 값을 가지고, 또한 동전의 앞면을 1, 뒷면을 0이라고 하면 이 또한 이산적인 값을 가진다고 볼 수 있다.
대표적인 이산확률분포의 종류로는 베르누이 분포, 이항분포, 초기하분포, 포아송분포, 기하분포, 음이항분포, 다항분포 등이 있다.
이산확률분포의 함수는 확률질량함수(pmf: probability mass function)라고 부른다.
다음으로, 연속확률분포는 가능한 값이 연속적인 구간을 가지며, 주로 실수형 값을 가진다. 예를 들어, 사람의 키, 몸무게, 온도 등 실수형 값을 갖는 확률분포가 바로 연속확률분포인 것이다. 대표적인 연속확률분포의 종류로는 정규분포, 표준정규분포 등이 있다. 연속확률분포의 함수는 확률밀도함수(pdf: probability density function)라고 부른다.
지금부터 다룰 내용은 이산확률분포 중 가장 기초가 되는 베르누이 분포에 대해서 알아보고자 한다.
베르누이 분포(Bernoulli Distribution)
베르누이 분포는 성공 확률이 일정한 1회의 시행(단일 시행)에서 나오는 확률분포로써 결과가 성공 또는 실패(다른 관점에서는 1 또는 0)과 같이 결과가 2가지의 경우만을 갖는 경우의 확률분포를 뜻한다. 이때, 성공 확률은 p로 나타내고 실패 확률은 1-p로 나타낸다.
베르누이 분포의 확률질량함수(pmf)는 다음과 같이 나타낼 수 있다.
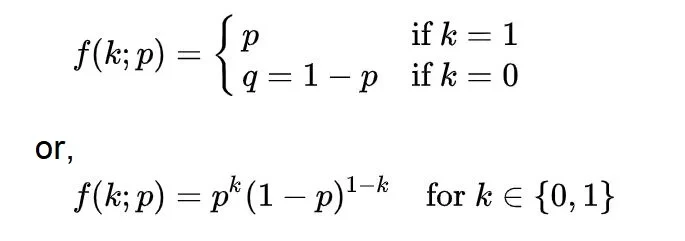
위 식을 다시 설명하면, k=1일 때(성공할 확률)는 p이고, k=0일 때(실패할 확률)는 1-p인 q이다.
베르누이 분포의 기댓값인 평균과 분산은 각각 다음과 같다.
- E(X) = p
- Var(X) = p(1-p)
베르누이 분포는 scipy의 stats 라이브러리의 bernoulli를 import해서 사용하면 파이썬 코드를 통해 시뮬레이션 할 수 있는데, 예를 들어 성공확률 p가 0.6인 경우 1000개의 샘플을 생성하여 성공과 실패의 확률을 히스토그램으로 시각화하면 다음과 같은 결과를 확인할 수 있다.

베르누이 분포의 기댓값은 p이므로 E(X)= p = 0.6이고 분산은 Var(X) = p(1-p) = 0.6 x 0.4 = 0.24이다.
결과를 보면 샘플로부터의 평균은 0.63, 분산은 0.23으로 이론적으로 계산했던 값과 거의 동일하다는 것을 확인할 수 있고, 시각화 결과를 보더라도 1(성공 확률)의 비율이 약 60%를 차지한다는 것을 확인할 수 있다.
이항분포(Binomial Distribution)
이항분포는 베르누이 분포와 매우 밀접한 관계가 있는 분포이다.
이항분포란 성공 확률이 일정한 n회의 시행(다중 시행)에서 나오는 확률분포이며, X는 이항분포를 따른다라는 표현으로 X~B(n, p)로 표기한다.
이항분포의 확률질량함수(pmf)는 베르누이 분포의 확률질량함수와 매우 유사하며 조합(combination)을 사용해서 다음과 같이 나타낼 수 있다.

이항분포의 기댓값인 평균과 분산은 각각 다음과 같다.
- E(X) = np
- Var(X) = np(1-p)
이항분포는 scipy의 stats 라이브러리의 binom을 import해서 사용하면 베르누이 분포를 시뮬레이션했던 것과 마찬가지로 파이썬 코드를 통해 시뮬레이션 할 수 있다. 아래 예시는 10번의 시행에서 각 시행의 성공 확률이 0.6인 이항분포의 시뮬레이션 결과이다.
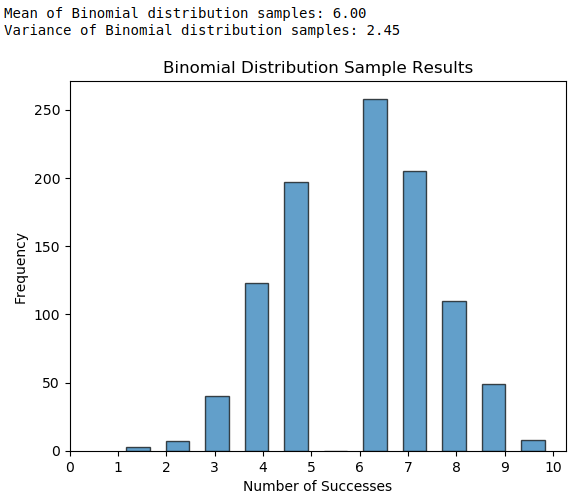
이항분포의 기댓값은 np이므로 10 * 0.6 = 6이고 분산은 np(1-p)이므로 10*0.6*0.4=2.4이다.
실제 시뮬레이션 결과를 보면 이론적 계산 결과와 거의 동일함을 확인할 수 있다.
또한, 실제 시각화 결과를 보더라도 성공 횟수가 6을 중심으로 분포되어 있고 0, 1, 10과 같은 극단적인 값은 상대적으로 적게 나타나는 것을 확인할 수 있고 정규분포와 흡사하게 종모양의 분포가 나타나는 것을 확인할 수 있었다.
BCE(Binary Cross Entropy)와 베르누이 분포의 관계: 인공지능 관점의 해석
오늘 학습한 베르누이 분포는 인공지능의 이진분류 문제에서 사용하는 손실함수인 Binary Corss Entropy(BCE)와 매우 깊은 연관관계를 갖는다. BCE는 인공지능 모델의 예측 확률 y^과 실제 레이블 y 사이의 차이를 측정하는 손실 함수로, 베르누이 분포에서 발생하는 데이터의 가능도(likelihood)를 최대화하는 것과 동일하다.
BCE의 수식은 다음과 같다.
- BCE(y, y^) = -(ylog(y^) + (1-y)log(1-y^)), 여기서 y는 실제 레이블(0 또는 1), y^은 모델이 예측한 클래스 1에 대한 확률이다.
가령, 고양이 이미지가 있는지 없는지 여부를 판별하는 모델이 있다고 가정했을 때, 모델이 80%의 confidence로 고양이가 있다고 예측했을 때, 실제 레이블이 1(고양이가 있음)이라고 가정하자.
이때 BCE 손실은 다음과 같이 계산된다.
BCE Loss = -(1log(0.8) + (1-1)log(1-0.8)) = -log(0.8) = 0.22
즉, 모델의 예측이 정확할수록 BCE Loss 값은 작아지고 모델을 학습하며 이 loss를 최소화하는 방향으로 학습함으로써 모델이 더욱 정확하게 예측할 수 있게 된다.
'Mathematics > Statistics' 카테고리의 다른 글
| 확률. 큰 수의 법칙 주사위 던지기 실험 - 코드 포함 (1) | 2024.01.22 |
|---|---|
| [Statistics] 확률과 확률분포 - 시행, 사건, 확률함수, 표본공간 (0) | 2023.08.02 |
| [Statistics] 기술통계: 이변량 자료의 정리 - 단순선형회귀분석(simple linear regression analysis) (0) | 2023.07.25 |
| [Statistics] 기술통계: 이변량 자료의 정리 - 상관분석(correlation analysis) (0) | 2023.07.25 |
| [Statistics] 기술통계: 일변량 자료의 분석 - 상자그림과 이상값 (2) | 2023.05.27 |
