논문 리뷰: DDPM(Denoising Diffusion Probablistic Models)
논문 링크: https://arxiv.org/pdf/2006.11239
깃허브 링크: https://github.com/lucidrains/denoising-diffusion-pytorch
오늘은 생성 모델의 혁신을 이끈 논문인 DDPM(Denoising Diffusion Probablistic Models)에 대해 논문 리뷰를 진행하고자 한다.
이 논문을 제일 처음 읽었을 때는 모르는 단어들과 수식들로 인해 큰 어려움을 겪었다. 하지만 여러 레퍼런스들을 참고하여 3주 정도 읽으니 어느 정도 남에게 설명할 수 있을 정도로 이해가 된 것 같다. 만약 독자들 중에서도 처음 디퓨전 논문을 읽고 너무 어렵다면 자주 반복해서 읽으면서 생성 모델의 원리, 기존 방식들과의 차이 그리고 근본적으로 왜 노이즈를 넣고 없애는 과정을 진행하는가에 관한 고민을 많이 해보면 점차 이 논문을 자기 것으로 만들 수 있을 것이다.
논문을 읽다 보면 수식의 늪처럼 느껴지지만, 본 논문 리뷰에서는 수학적인 증명보다는 전체적인 컨셉을 이해하는데 초점을 맞춰 리뷰를 진행하도록 한다.
1. Background

2020년 이전까지만 하더라도 VAE, GAN이 생성 모델의 패러다임을 주도하고 있었다. 물론, 2015년에 ICML에 발표된 논문인 "Deep unsupervised learning using nonequilibrium thermodynamics"에서 디퓨전 모델의 초기 개념이 제안되었으나 디노이징 과정의 효율성이 부족했고 실제 응용에 쓰기에는 부족했기 때문에 여전히 GAN과 VAE가 생성 모델의 주요 접근법으로 자리 잡고 있었다.
그런데 2020년, NIPS에 "Denoising Diffusion Probablistic Models(DDPM)" 논문이 발표되면서 생성 모델은 GAN과 VAE를 뛰어넘는 성능을 보여주었고, 강력한 생성 모델로써 패러다임을 주도하게 된다. 대표적으로 GLIDE, DALL-E 2, Imagen과 같은 이미지 생성 모델이 디퓨전 기반의 모델이다.
위 그림의 우측을 보자. DALL-E 2에서 말을 타고 있는 우주인을 photorealistic한 style로 그려달라고 하니 꽤 사실적인 그림이 생성된 것을 볼 수 있다. 그리고 Imagen의 경우, 뇌가 로켓을 타고 달을 향하도록 그림을 그려달라고 하자 창의적이면서 재미있는 그림이 생성된 것을 볼 수 있다.

위 그림을 보자. 위 그림은 실제 이미지일까? 아니면 생성 모델이 생성한 이미지일까? 정답은 생성 모델이 생성한 이미지이다.
DDPM 논문을 보면 생성된 샘플이라고 적혀있는 것을 확인할 수 있다. 왼쪽으로부터 2열까지는 CelebA-HQ 데이터셋으로부터 샘플링된 샘플인데 진짜 사람같이 보이는 사진을 생성해내는 놀라운 성능을 볼 수 있다.
더 많은 예시들은 아래 논문에서 확인할 수 있다.


위 그림은 일반인들도 쉽게 사용할 수 있는 Stable Diffusion의 overall architecture를 나타낸다. 특정 텍스트가 prompt로 들어오면, CLIP 등으로 구성된 텍스트 인코더를 통해 Token embeddings을 생성하고, 이를 Image Information Creator인 Diffusion에 통과시킨다. 이 Diffusion Model은 UNet과 Scheduler로 구성되어 있다. 디퓨전을 통과하고 나면 이미지 정보 텐서가 이미지 디코더로 들어가게 되고 디코더를 통해 최종적인 이미지가 생성된다. DALL-E 2나 Imagen도 이와 비슷한 프로세스를 거치기 때문에, 우리의 핵심은 중앙에 있는 Diffusion Process를 이해하는 것이다.
흔히 AI를 공부하게 되면 모델을 크게 회귀 모델과 분류 모델로 나누고 이 둘을 기반으로 공부하게 된다.
그런데 디퓨전과 같은 생성 모델은 근본적으로 이와 매커니즘이 다르다.
가령, 어떤 이미지가 입력으로 들어왔을 때, 클래스를 예측하는 분류 모델이라 가정해보자.
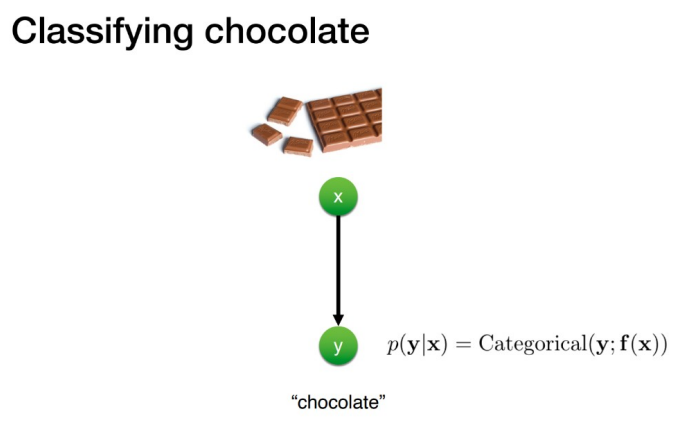
위 그림에서 x는 입력 이미지인 초콜릿 이미지, y는 이에 해당하는 라벨인 초콜릿이라 가정하자.
이때, 초콜릿 이미지라는 x가 주어졌을 때, 초콜릿이라는 클래스일 조건부 확률로 나타낼 수 있다.
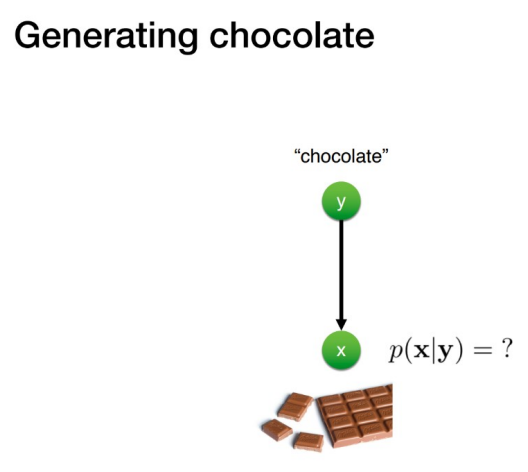
이와 반대로, 생성 모델은 초콜릿이라는 클래스가 주어졌을 때, 이에 해당하는 원본 이미지 x인 조건부 확률로 condition이 뒤바뀌게 된다.

즉, 분류 모델의 경우 x가 주어졌을 때 y일 확률이 가장 높은 클래스를 예측하는 것이 목표지만 생성 모델은 조건을 보고 추정을 통해 원본에 해당하는 x를 샘플링하는 것이 목표라는 아주 큰 차이점이 있다.
생성 모델에 대해 나동빈님의 GAN 강의 자료를 참고해서 조금 더 깊게 이해해 보자.


생성 모델은 실제로 존재하지 않지만 마치 실제로 존재하는 것 같은 이미지를 생성한다.
또한, 이러한 생성 모델은 결합 확률 분포(joint probablity distribution)을 학습하여 새로운 데이터 인스턴스를 샘플링하는 구조로 이루어져 있다.
가령, 사람의 얼굴을 생성하는 모델이 있다고 가정하자. 이때, 사람의 특징을 코의 크기와 눈의 모양과 같이 2개의 특징과 특정 결합 확률의 밀도로 구성된 3차원 특징 공간의 확률 분포로 구성할 수 있다. 이렇게 구성된 그래프에서 사람 이미지, 즉, 새로운 데이터 인스턴스는 이 다차원 특징 공간 상의 한 점으로 표현할 수 있게 된다.
만약 결합 확률 분포 상의 확률 밀도가 높은 영역에서 샘플링하게 된다면 실제 사람 얼굴처럼 보이는 인스턴스를 생성하게 되지만 반대로, 확률 밀도가 낮은 영역에서 샘플링하게 된다면 사실성이 떨어진 인스턴스를 생성하게 되는 것이다.
즉, 생성 모델의 품질은 원본 데이터의 확률 분포를 얼마나 잘 근사시키는지에 따라 달라지게 된다. 쉽게 이해하기 위해 아래 그림을 보자.

위 그림에서, 왼쪽의 p(·)는 실제 데이터 분포를 나타내고 x(1), x(2), x(3), x(4)는 데이터 샘플을 의미한다. 그리고 q_θ(·)는 미지의 확률 분포 p(x)에서 훈련 데이터 D = {x(1), x(2), x(3), x(4)}가 추출되었을 때, 이 데이터를 통해 p(x)와 가까운 확률분포를 학습하는 생성 모델이다.
즉, 생성 모델의 경우 원본 데이터 분포를 잘 근사하는 확률분포를 학습하는 것이 목표이다.

위 그림에서 초기 생성 모델의 분포는 초록색의 분포이고, 원본 데이터의 분포는 검은색 점으로 구성된 가우시안 형태의 분포일 때, 생성 모델을 학습시킨다고 가정하자. (a) ~ (d) 시점으로 가면 갈수록 모델은 점차 원본 데이터의 분포를 학습하게 되고, 생성 모델이 잘 학습되었다면 원본 데이터의 분포를 아주 잘 근사화하도록 학습되게 되고, 아래 그림의 빨간 네모 박스의 샘플들처럼 사실적인 이미지를 생성할 수 있게 된다.

이제 본격적으로, 디퓨전 모델에 대해서 알아보자.

디퓨전(diffusion)이라는 용어는 초기 상태의 분자들이 점차 흩어지는 랑주뱅 동역학(langevin dynamics)에서 영감을 받아 사용하게 되었고, 디퓨전 모델은 원본 데이터에 점차 노이즈를 삽입하여 가우시안 형태의 단순한 분포로 변환하고 이를 다시 복원하는 과정을 따른다.
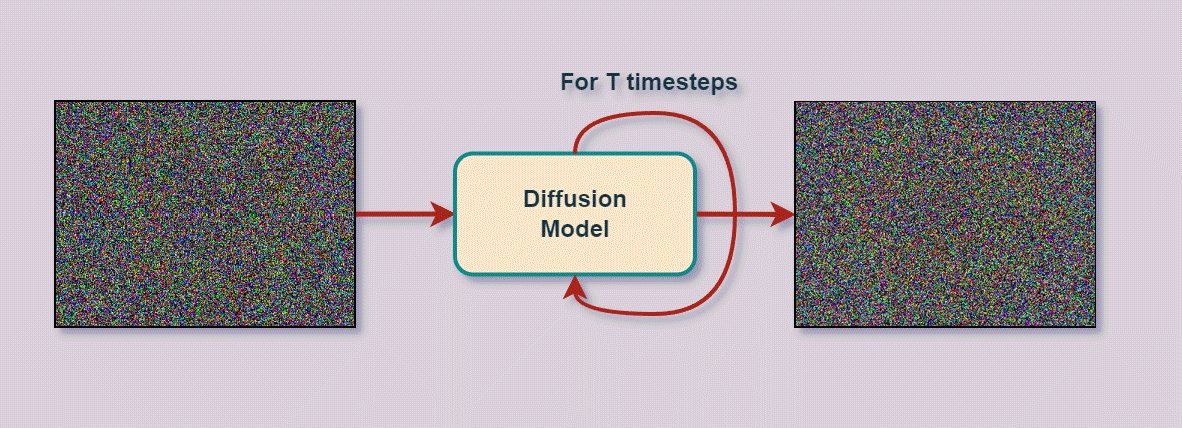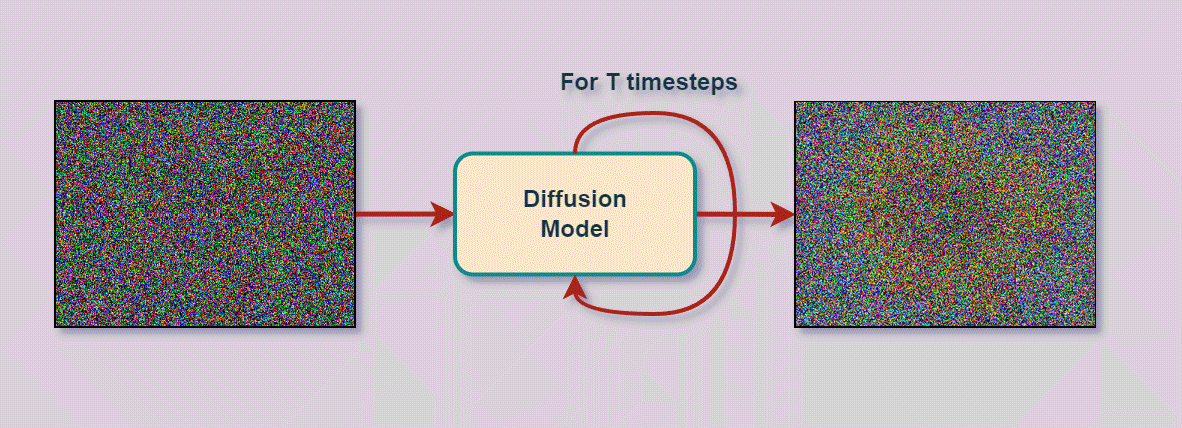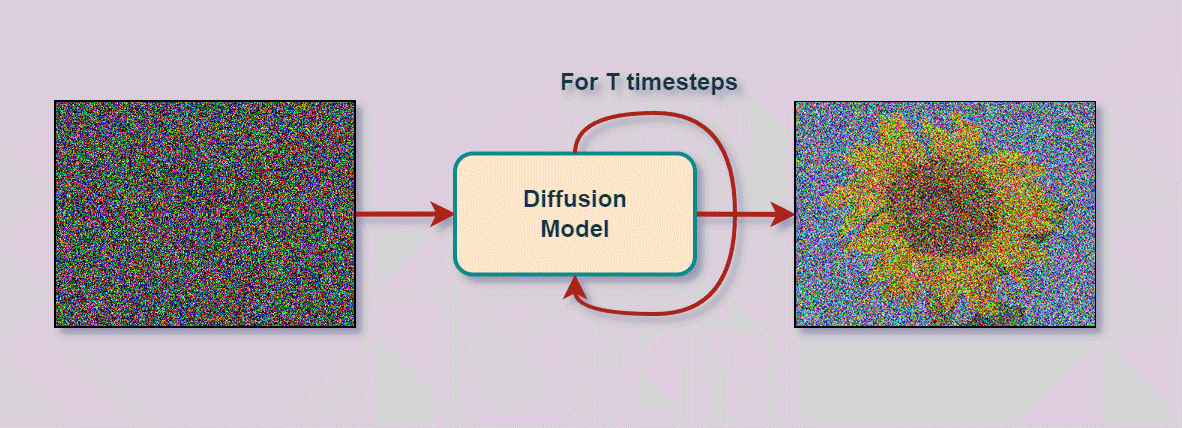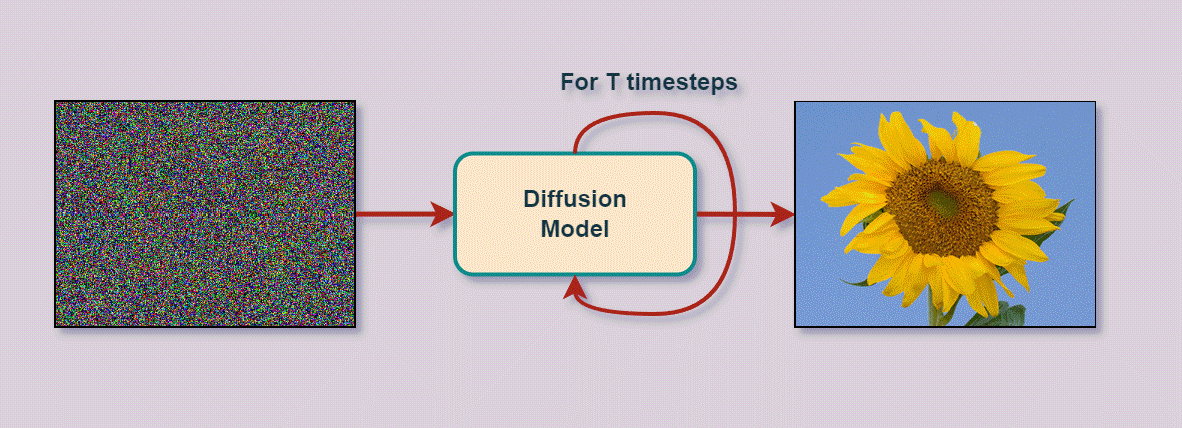

위 그림을 보면 'An RGB image of a Sunflower' 이라는 텍스트가 입력되었을 때, T번의 타임 스텝 동안의 디퓨전 프로세스와 디노이징 프로세스를 거쳐 RGB 이미지 형태의 해바라기 사진을 생성하는 과정을 보여준다.

즉, 디퓨전 모델은 원본 이미지 x_0가 있을 때, 전체 타임 스텝 T까지 점차 노이즈를 삽입하는 디퓨전 프로세스 q와 X_T부터 x_0까지 역으로 노이즈를 점차 없애며 이미지를 복원하여 사실적인 이미지를 생성하는 과정인 리버스 프로세스 확은 디노이징 프로세스 pθ로 구성되어 있다.
2. Denoising Diffusion Probablistic Models (DDPM)
DDPM을 제대로 이해하기 위해선 Background가 상당히 중요하기 때문에 서론이 길었다.
하지만 전반적인 생성 모델의 컨셉을 이해하기 위해 지금까지 탄탄한 background를 형성했기 때문에 DDPM을 꼭 이해할 수 있을 것이다. Experiments에 대한 내용은 논문에 잘 적혀있으니 생략하고 핵심 Method 부분에 대해서 깊게 이해해보는 것이 본 리뷰의 목표이다. DDPM 리뷰의 핵심인 이번 section에서는 수학적 배경을 위한 Prerequisite, Denoising Diffusion, Diffusion Process, Reverse Process에 대해서 설명하고자 한다.
2.1 Prerequisite


본 논문을 이해하기 위해서 학부 수준의 기초 통계학의 내용, 베이지안 룰, 가우시안 분포, 가우시안 분포의 확률 밀도 함수(pdf), 테일러 급수, 마르코프 성질에 관한 기본 내용을 알고 있다면 본 논문을 이해하는데 있어 한결 수월해진다.
본 리뷰에서는 중요한 두 개의 성질에 대해서만 간단히 설명하겠다.
마르코프 성질은 특정 상태(t+1 시점)의 확률은 오직 현재 상태(t)에만 의존한다는 것이다.
다음으로, 가우시안 분포에서 평균인 μ와 분산인 σ^2 값에 따라서 가우시안 분포의 형태가 어떻게 달라지는지 안다면 머릿속으로 디퓨전 프로세스를 상상할 때 큰 도움이 된다. 간단히 설명하자면, 평균 μ의 값이 0이고 분산 σ^2의 값이 1이라면 우리가 흔히 알고 있는 표준 정규분포 형태를 따르게 되며 위 그림에서 왼쪽은 분산은 고정하고 평균 μ만 다르게 한 것이고, 오른쪽은 평균은 고정하고 분산 σ^2을 다르게 한 것이다. 평균 μ는 정규분포의 중심 위치를 정하며, 분산 σ^2은 분포의 폭과 높이를 정한다. 분산이 크면 클수록 분포의 높이는 낮아지며 폭은 넓어지게 된다.
2.2 Denoising Diffusion

이제 본격적으로 디노이징 디퓨전 모델이 무엇인지 살펴보자.
앞에 background에서 살짝 언급한 것과 같이 디노이징 디퓨전 모델은 심플한 2개의 프로세스로 구성되어 있다.
첫 번째는 Forward Diffusion Process로, 입력 이미지에 마르코프 성질에 따라 점진적으로 노이즈를 추가하는 과정이다.
다음으로 Reverse Denoising Process는 무작위한 노이즈 상태의 X_T 시점에서 마르코프 성질에 따라 점진적으로 노이즈를 없애는 과정이다.

디퓨전 과정 q(X_t | X_(t-1))로부터 얻어진 디노이징 과정의 q(X_(t-1) | X_t)의 조건부 확률은 그 자체만으로 샘플링, 즉 inference에 사용할 수 없다. 하지만 이전 연구를 통해 만약 q(X_t | X_(t-1))<노이즈를 넣은 것>이 가우시안이라면, q(X_(t-1) | X_t) 또한 가우시안이라는게 밝혀졌다. 단, β가 아주 작아야한다는 조건이 있다. 본 논문에서는 β 기호가 계속 나오는데, 이는 사실 분산인 σ^2을 뜻한다. 이게 무슨 소리인지 처음 읽으면 매우 이해하기 난해하다. 다음 그림을 통해 한번 다시 파고 들어보자.

노이즈를 점진적으로 추가하는 Diffusion Process는 코드 상 간단하게 구현할 수 있지만, 노이즈가 포함된 시점에서 이전 시점의 확률 분포를 예측하는 것은 쉽지 않다.
디노이징 과정에서는 q(X_(t-1) | X_t), 즉 현재 시점 t의 데이터를 기반으로 t-1 시점의 데이터를 복원해야 하지만 이를 수학적으로 계산하는 것은 매우 복잡하고 어려운 문제이다.
대신, Forward Process에서 노이즈의 크기인 β를 매우 작게 설정하여 q(x_t | x_(t-1))가 가우시안 분포라는 가정을 만족시킨다. 이를 활용하여 q(X_(t-1) | X_t)를 가우시안 분포로 근사하는 pθ를 학습시켜야 한다.
이때, 가우시안 분포를 따른다는 점을 이용하여 Forward Process를 통해 얻은 조건부 확률 분포를 베이지안 룰을 통해 q(x_(t-1) | x_t)에 대한 가우시안 근사를 구하고 모델이 학습하는 pθ 간의 확률 분포 차이를 KL Divergence를 활용하여 확률 분포 차이를 최소화하도록 학습하는 것이 디노이징 디퓨전 모델의 목표이다.
이 과정을 그림으로 나타내면 다음과 같다.

2.3 Diffusion Process
이제 노이즈를 점진적으로 추가하는 과정인 Forward Diffusion Process를 살펴 보자.

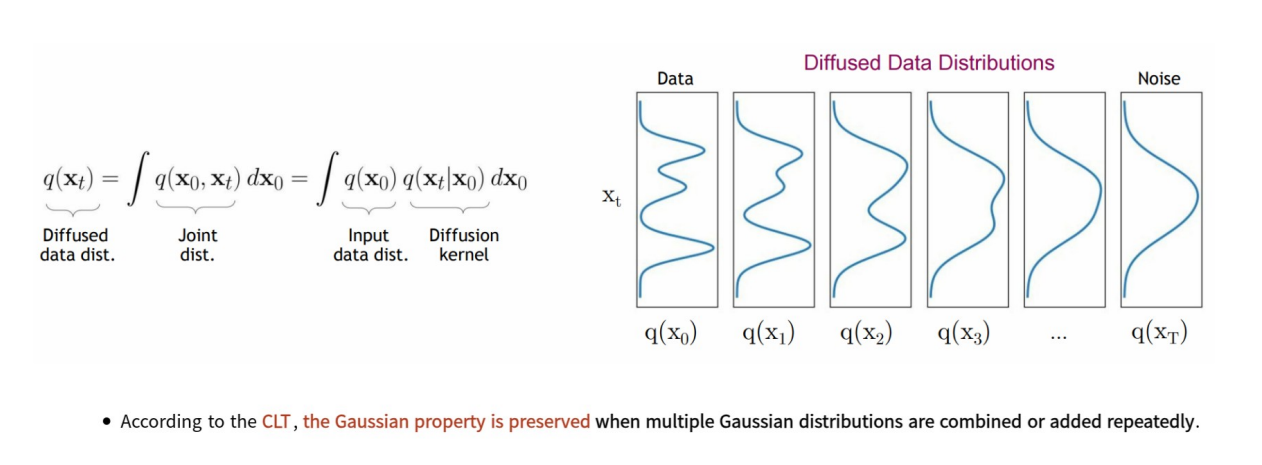
위 그림에서 가장 초기 x_0 시점에서는 원본 고양이 이미지가 있다. 하지만 마르코프 성질에 따라 매 스텝마다 작은 크기의 β 만큼의 가우시안 노이즈가 추가되면서 X_T 시점에서는 완전 noisy한 상태가 되고 가우시안 분포를 따르게 된다.
이 과정은 중심 극한 정리(CLT)에 의해 성립하게 되는데, 이는 가우시안 분포는 반복적으로 결합되거나 추가되더라도 가우시안 성질이 보존되며, 각 시점에서 분포가 점차 변화하는 과정을 통해 초기의 복잡한 데이터 분포가 가우시안 분포로 수렴하게 된다는 것이다.
각 시점별로 분포가 변화하는 것을 보면 초기의 복잡한 분포에서 가우시안 분포로 변화하는 것을 확인할 수 있다. 즉, 생성 모델은 결국 분포로부터 샘플링해야 하는데 Forward Diffusion Process를 통해 복잡한 분포를 아주 simple한 분포로 변환할 수 있고, 이 분포로부터 sampling하여 높은 품질의 이미지를 생성할 수 있도록 한다.

또한, β_t는 노이즈의 크기를 표현하는 scailing factor인데 본 논문에서는 각 스텝에서 노이즈의 크기를 정하는 과정을 Noise Scheduling이라고 표현한다. 크게 3가지 정도로 실험을 진행했는데 선형적으로 증가시키는 방식과 시그모이드 형태로 증가시키는 방식, 이차함수 형태로 증가시키는 방식으로 진행했다.
먼저, Linear scheduling (선형 스케줄링)은 β_t 값이 선형적으로 증가하는 형태로, 초기에는 노이즈의 크기가 작게 추가되며, 스텝이 진행됨에 따라 점진적으로 노이즈가 증가한다.
다음으로, Sigmoid scheduling (시그모이드 스케줄링)은 β_t 값이 시그모이드 형태로 증가하는데 초기에는 노이즈 증가가 느리게 진행되다가, 중간 지점에서 급격히 증가한 후 다시 느려진다.
마지막으로, Quadratic scheduling (이차 스케줄링)은 β_t 값이 이차함수 형태로 증가하여 초기에는 노이즈 증가가 선형보다 느리고, 후반부로 갈수록 빠르게 증가한다.
β_t의 스케줄링 방식은 생성 모델의 성능에 큰 영향을 미치기 때문에 데이터 분포나 모델의 특성에 따라 적합한 방식을 선택할 수 있다. 예를 들어, Sigmoid 스케줄링은 초기 정보를 더 오래 유지하며, Quadratic 스케줄링은 빠르게 노이즈를 추가하고자 할 때 유리하다.

지금까지 이해한 내용을 기반하여, 최종적으로 Forward Diffusion Process의 수식을 보면 다음과 같이 정의할 수 있다.
계속 β를 사용하다가, 최종 수식에서는 α가 등장했는데 이는 실제 계산을 간단히 하기 위해 1-β_t를 α로 정의하며 각 시간 t에서 데이터 유지 비율을 나타낸다.
α bar_t의 경우, 모든 이전 스텝의 α_s 값을 누적하여 곱한 값으로 누적 데이터 유지 비율을 나타낸다. 시간이 지남에 따라 α bar_t는 점차 감소하여 원본 데이터 정보가 줄어들고, 노이즈가 점차 지배적이 된다.
즉, 수식에서 이 둘을 사용하는 이유는 스텝에서의 데이터 유지와 노이즈 추가를 간단히 표현할 수 있기 때문이다.
2.4 Reverse Process

이제 DDPM의 핵심인 Reverse Process이다. 소설가인 Pearl S. Buck은 "It's easy to destroy but hard to create."라는 명언을 남겼다. 이는 디노이징 디퓨전 모델의 Reverse Process에 아주 적합한 말인 것 같다. 파괴하는 것은 쉽지만 만드는 것은 어렵다.
먼저, 아주 쉽게 확률 분포의 공간의 개념으로 Reverse Process를 이해해보자.

다음 그림과 같이 Forward Diffusion 과정을 통해 원본 데이터의 부분 공간으로부터 벗어난 전체 공간 상의 한 점으로 샘플을 나타낼 수 있다. 우리는 이 샘플을 Reverse Diffusion 과정을 통해 최대한 원본 데이터의 확률 분포 공간으로 복원시키고 이를 샘플링해야 높은 품질의 이미지를 생성할 수 있게 된다.

이와 같이 생성에 활용되는 조건부 확률 분포 pθ를 학습하기 위해 바로 직전에 소개한 Diffusion Process q(z|x)의 조건부 확률 분포가 활용된다. 모델 학습을 위해 사용되는 Loss를 통해 살펴보자.

먼저, 가장 위의 Loss_diffusion은 2015년에 발표된 논문인 디퓨전의 시초인 "Deep unsupervised learning using nonequilibrium thermodynamics"에 제안된 loss function을 깔끔하게 다시 정리한 것이다. 총 3가지 term으로 구성되어 있는데,
첫 번째 loss term은 KL Divergence를 통해 x_0로 x_T인 z를 생성하는 q 분포와 pθ(z)의 분포가 유사해지도록 하는 Regularizer on Encoder이다.
다음으로 두번째 loss term은 reverse process와 diffusion process 간의 분포가 유사해지도록 하는 Denoising Process이다.
마지막으로, 세 번째 loss term은 Reconstruction loss로 x_1에서 x_0이 나올 likelihood를 maximization하는 loss term이다.

하지만 본 논문에서는 이 3개의 loss term을 다음과 같이 DDPM Loss를 제안함으로써 단순히 노이즈를 비교하는 형태로 단순화하였고 이는 이 논문의 가장 큰 contribution이라고 할 수 있다. 조금 더 심플하게 살펴보면, forward process로 추가된 노이즈와 모델이 예측한 노이즈 간의 MSE를 계산하는 아주 단순한 형태의 loss로 간소화시켰다는 것을 확인할 수 있다.
수식에 대한 자세한 정리 부분은 appendix에 첨부하였으니 참고해보면 좋을 것 같다.

결국, 본 논문에서는 해당 loss를 통해 모델이 forward process를 통해 추가된 노이즈 ε을 정확히 예측하도록 학습하고, 학습된 ε_θ를 사용해 forward process의 반대 방향으로 점진적으로 원본 데이터를 복원하여 샘플링한다.
이는 앞에서 소개한 scheduling 방법과 U-Net을 결합하여 구현할 수 있다.
많은 Network Architecture 중에 U-Net을 사용하는 이유는 U-Net은 노이즈 제거와 이미지 복원에 필요한 전역적 그리고 국소적 정보를 처리하는 데 강점을 가지며, 효율적이고 유연한 구조를 갖고 있기 때문이다.

마지막으로 아래 그림은 지금까지 설명한 Forward Diffusion Process와 Reverse Diffusion Process를 전체적으로 보여주는 그림이다.
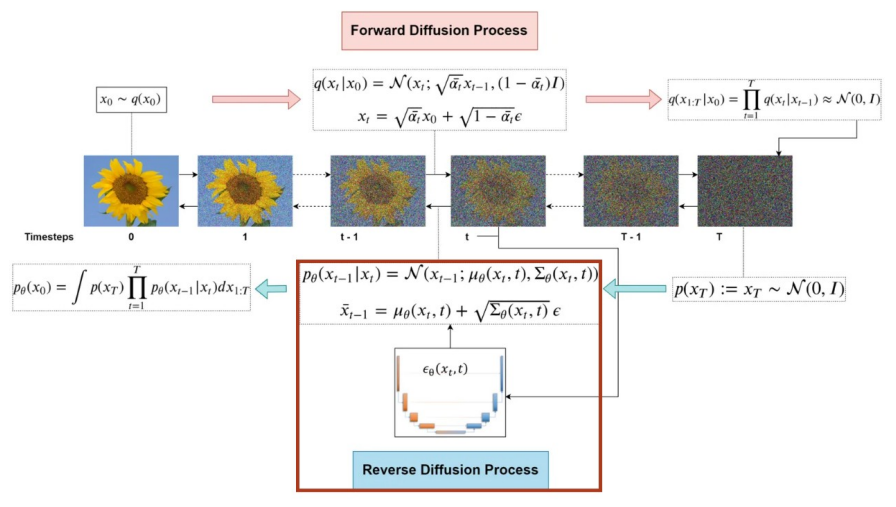
논문이 상당히 난이도가 높고, 논문 자체에는 수식이 너무 많고 VAE나 Flow-based Model을 모른다면 수식 유도가 어렵기 때문에 수식을 하나하나 다 이해하려고 하는 것보다 논문의 key idea를 확실하게 이해하는 식으로 진행하는 것도 괜찮은 것 같다.
Appendix






Reference
[1] YouTube. Denoising diffusion probabilistic models explained. Retrieved from https://www.youtube.com/watch?v=AVvlDmhHgC4
[2] Stanford University. (2023). Lecture 15: Diffusion models. CS231n: Deep Learning for Computer Vision. Retrieved from https://cs231n.stanford.edu/slides/2023/lecture_15.pdf
[3] Lazebnik, S. (2023). Lecture 17: Diffusion models. Retrieved from https://slazebni.cs.illinois.edu/spring23/lec17_diffusion.pdf
[4] OpenCV. Denoising diffusion probabilistic models. Retrieved from https://learnopencv.com/denoising-diffusion-probabilistic-models/
[5] Sohl-Dickstein, J., Weiss, E. A., Maheswaranathan, N., & Ganguli, S. (2015). Deep unsupervised learning using nonequilibrium thermodynamics. International Conference on Machine Learning (ICML), 2256–2265. Retrieved from https://arxiv.org/abs/1503.03585
[6] Ho, J., Jain, A., & Abbeel, P. (2020). Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems (NeurIPS). Retrieved from https://arxiv.org/abs/2006.11239
[7] YouTube. The diffusion model: A new paradigm in AI Retrieved from https://www.youtube.com/watch?v=_JQSMhqXw-4
'Paper' 카테고리의 다른 글
| [Paper Review] Disrupting Deepfakes: Adversarial Attacks ~ (9) | 2024.10.01 |
|---|---|
| [Paper Review] Explaining and Harnessing Adversarial Examples(FGSM) (2) | 2024.08.30 |
| Face Identification, Recognition, Verification 오픈소스 정리 (0) | 2023.08.24 |
| [Paper] Face Recognition 관련 논문 정리 (0) | 2023.08.24 |
