로지스틱 손실 함수
선형 회귀는 정답과 예상값의 오차 제곱(y-y^)^2이 최소가 되는 가중치와 절편을 찾는 것이 목표였다.
반면, 로지스틱 회귀 분류의 목표는 올바르게 분류된 샘플 데이터의 비율 자체를 높이는 것이 분류의 목표이다.
올바르게 분류된 샘플의 비율은 미분 가능한 함수가 아니기 때문에 경사 하강법의 손실 함수로 사용할 수 없다. 이 때 사용할 수 있는 함수가 바로 로지스틱 손실 함수이다.
로지스틱 손실 함수는 다중 분류를 위한 손실 함수인 크로스 엔트로피(cross entropy) 손실 함수를 이진 분류 버전으로 만든 것이다.
엔트로피의 개념
기본적인 엔트로피의 개념을 살펴보면, 엔트로피(=불확실성)에서 사용하는 함수는 로그 함수인데
확률이 p일 때, 엔트로피 함수는 plogp 이다.
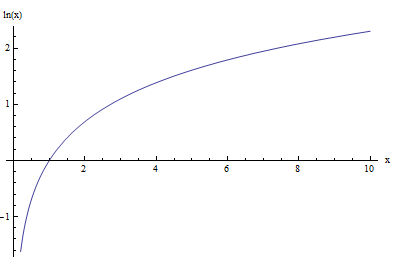
위 그래프는 기본적인 로그 함수인 log x의 그래프이다.
로그 함수는 x가 0으로 가까워질수록 -∞에 가까워지고 x가 1일때 0이 된다.
위 성질을 이용하면, 확률이 1보다 작으면 엔트로피 전체의 값은 점점 -∞에 가까워지고 확률이 1일때 0이 된다.
이제 엔트로피 함수 앞에 '-'기호를 붙여줘 -plogp 와 같이 만든다면,
확률이 1보다 작으면 점점 ∞에 가까워지고 확률이 1일때 0이 된다.
즉, 확률이 작으면 작아질수록 일어날 수 있는 경우의 수가 많아지고 이로 인해서 불확실성이 커진다.
크로스 엔트로피의 개념
예측값(활성화 함수가 출력한 값)을 a라고 하고, 정답값(타깃)을 y라고 할 때, 크로스 엔트로피는 아래와 같이 정의된다.
-(ylog(a) + (1-y)log(1-a))
식이 복잡해 보이는데 사실 어렵지 않다.
예를 들어, 정답은 1인데 0으로 예측했다고 가정하자.(완전히 잘못 예측한 예시)
-(1log(0) + (1-1)log(1))
-(-∞ + 0)
= ∞ → 즉, 정답값이 예측값과 완전 틀릴 경우, 손실함수는 무한대가 된다.
반대로, 잘 맞춘 경우를 예를 들어보자.
예를 들어, 정답도 1이고, 예측한 값도 1이라고 해보자.
-(1log(1) + (1-1)log(1-1))
= 0 → 즉, 정답값이 예측값과 일치할 경우, 손실함수는 0이 된다.
- 이진 분류: binary_crossentropy
- 다중 분류: sparse_categorical_crossentropy
로지스틱 손실 함수
로지스틱 손실 함수는 다음과 같다. 이때, a는 활성화 함수가 출력한 값이고, y는 타깃이다.
L = -(ylog(a) + (1-y)log(1-a))
위 식을 더 쉽게 나타내면, 이진 분류는 그렇다(1), 아니다(0)이라는 2개의 정답만 있는데 즉, 타깃의 값은 1 또는 0이다.
따라서 위 식을 아래와 같이 정리할 수 있다.
| L | |
| y가 1인 경우(양성 클래스) | -log(a) |
| y가 0인 경우(음성 클래스) | -log(1-a) |
크로스 엔트로피의 예시를 통해 확인할 수 있듯이 두 식의 값을 최소로 만들다 보면, 예측값인 a의 값이 우리가 원하는 목표치가 된다는 것을 알 수 있다.
예를 들어 양성 클래스인 경우 로지스틱 손실 함수를 최소로 만들려면 a는 자연스럽게 1에 가까워지고 음성 클래스인 경우 로지스틱 손실 함수의 값을 최소로 만들면 a가 0에 자연스럽게 가까워진다.
이 값을 계단 함수에 통과시키면 올바르게 분류 작업이 수행된다. 즉, 로지스틱 손실 함수를 최소화하면 a의 값이 가장 이상적으로 생각하는 값이 된다.
로지스틱 손실 함수 미분
로지스틱 손실 함수를 미분하여 가중치와 절편에 대한 로지스틱 손실 함수의 미분 결과는 다음과 같다.
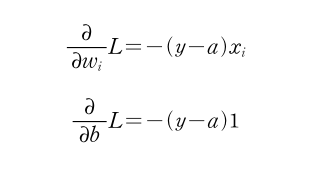
미분한 결과를 자세히 보면 선형회귀에서의 예측 값인 y^가 로지스틱 회귀에서는 a로 바뀌었을 뿐 제곱 오차를 미분한 결과와 동일함을 확인할 수 있다. 아래의 표를 통해 살펴보자.

로지스틱 손실 함수와 연쇄 법칙
미분에서는 합성 함수의 도함수를 구하기 위한 방법으로 연쇄 법칙(Chain Rule)이 있다.
- 예를 들면 y=f(g(x)) 일 때, y를 x에 대해 미분하는 방법은 y를 u에 대해 미분한 값과 u를 x에 대해 미분한 값을 곱하는 것인데 이게 연쇄법칙이다.

이때, 로지스틱 손실 함수(L)를 가중치 w와 절편 b에 대하여 바로 미분하면 너무 복잡하기 때문에 아래와 같이 연쇄 법칙을 이용하면 곤란한 문제를 해결할 수 있다.

그림을 보면, 로지슽기 손실 함수(L)를 활성화 함수의 출력값(a)에 대하여 미분하고, 활성화 함수 출력값(a)은 선형 함수의 출력값(z)에 대하여 미분하고, 선형 함수의 출력값(z)은 가중치(w) 또는 절편(b)에 대하여 미분한 다음 서로 곱하면 결국 로지스틱 손실 함수를 가중치에 대해 미분한 결과를 얻을 수 있다.
이 과정은 위 그림에서 가장 오른쪽부터 왼쪽으로 역방향으로 진행된다는 것 또한 확인할 수 있다.
이렇게 로지스틱 손실 함수에 대한 미분이 연쇄 법칙에 의해 진행되는 구조를 보고 '그레이디언트가 역전파된다'고 말한다.
이제 차례대로 로지스틱 손실 함수(L)를 a에 대해 미분하고, a를 z에 대해 미분하고, z를 w에 대해 미분하면 된다.
이러한 계산이 끝나면 각 단계에서 구한 도함수를 곱하여 로지스틱 손실 함수를 w에 대하여 미분하면 된다.
로지스틱 손실 함수를 w에 대하여 미분
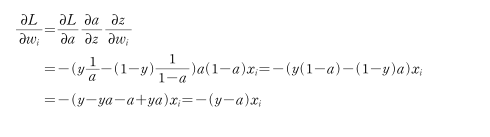
결과를 확인하면 로지스틱 손실 함수를 wi에 대해 미분한 결과는 제곱 오차를 미분한 결과와 일치함을 확인할 수 있다.
가중치 업데이트 방법 정리
로지스틱 회귀의 가중치(w)를 업데이트 하려면 로지스틱 손실 함수(L)를 가중치(w)에 대해 미분한 식을 가중치(w)에서 빼면 된다.

절편 업데이트 방법 정리
로지스틱 손실 함수를 절편에 대하여 미분하는 방법도 연쇄 법칙(chain rule)을 이용하면 쉽게 구할 수 있다.

로지스틱 회귀의 절편(b)을 업데이트 하려면 로지스틱 손실 함수(L)를 절편(b)에 대해 미분한 식을 절편(b)에서 빼면 된다.

'AI & BigData' 카테고리의 다른 글
| [AI] 테스트 세트로 모델을 튜닝하면 안되는 이유 (0) | 2023.07.25 |
|---|---|
| [AI] 사이킷런을 활용해 훈련 세트와 테스트 세트로 나누기 (0) | 2023.06.22 |
| [AI] YOLOv5를 활용한 히잡, 마스크 객체 인식 실습 (0) | 2023.06.03 |
| [AI] 당뇨병 환자의 1년 후 병의 진전된 정도를 예측하는 모델 만들기 - 1 (0) | 2023.05.26 |
| [AI] 선형회귀분석(Linear regression) (0) | 2023.05.23 |
