[Linear Algebra] SVD(특이값 분해)

특이값 분해(Singular Value Decomposition)

특이값 분해는 행렬(matrix ~ data)을 특이값(singular value)을 가지는 행렬로 분해하는 것이다. 특이값 분해는 데이터를 차원 축소하거나 노이즈를 제거하는 데에 유용하게 사용되며, 다양한 응용 분야에서 활용된다.

 

자, 먼저 특이값 분해를 학습하기 전에 특이값이 무엇인지 알아보자.

 

특이값(Singluar Value)

특이값을 이해하기 위해서는 먼저 고유값에 대해 알아보는 과정이 필요하다.

- 고유값(eigenvalue)

>> 정방행렬에서 대각성분 빼고 모두 0인 행렬, 즉 대각행렬에서 대각성분들을 고유값(eigenvalue: 아이겐밸류)이라고 한다.

만약 아래와 같은 3x3 행렬이 있다고 가정해 보자.

[[1, 0, 0],

 [0, 4, 0],

 [0, 0, -2]]

이 경우 고유값은 1, 4, -2가 된다.

 

- 특이값(singluar value)

>> 고유값은 정사각형 모양인 행렬, 즉 정방행렬(n x n matrix)에서 대각성분을 제외하고 나머지가 모두 0인 경우 그 대각성분들이 특이값(singular value)이 된다.

예를 들어 아래와 같이 4x3 행렬과 3x5 행렬이 있다고 가정해보자.

1번 예시: 4x3 matrix

[[1, 0, 0],

 [0, 4, 0],

 [0, 0, -3],

 [0, 0, 0]]

이 경우 특이값은 1, 4, -3이다.

 

2번 예시: 3x5 matrix

[[1, 0, 0, 0, 0],

 [0, 4, 0, 0, 0],

 [0, 0, -3, 0, 0]]

이 경우 특이값은 1, 4, -3이다.

 

SVD(Singular Value Decomposition)

https://webdocs.cs.ualberta.ca/~rgreiner/RESEARCH/OLD-BiCluster/SVDApproaches.html

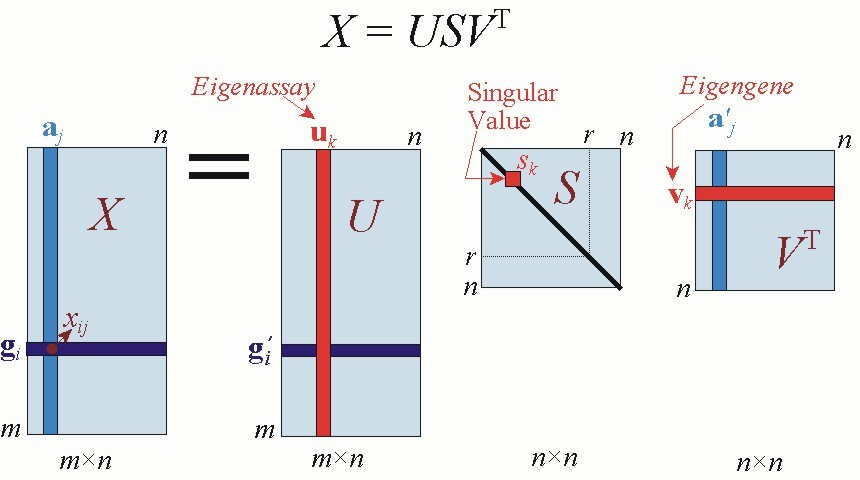
앞에서도 설명했듯이 SVD는 행렬 A를 USV 행렬곱으로 분해하는 것이다.

쉽게 설명하면 어떤 행렬이 주어지면 그 행렬은 U * S * VT로 분해할 수 있다는 것이고 이때 가운데에 있는 S는 항상 대각성분만 숫자고 나머지는 0인 행렬이 된다는 것이다.

https://towardsdatascience.com/simple-svd-algorithms-13291ad2eef2

 

- 추가 학습 후 이어서 작성 예정