[Linear Algebra] 벡터의 내적과 노름

내적(dot product)

고등학교 시절 기하와 벡터 과목을 이수했다면 한번쯤 벡터의 내적이라는 말을 들어본 적이 있을 것이다. 내적을 구해서 어디에 쓰는 것일까? 내적을 구하면 두 벡터 간의 닮은 정도를 알 수 있다.
가령 벡터 u와 벡터 v가 있을 때, 내적은 벡터끼리의 곱의 한 종류로 아래와 같이 각 요소끼리 곱한 값을 총합해서 정의한다. 즉, u·v = ||u||·||v||·cosθ = ||u||·cosθ·||v|| = ||v||·cosθ·|u|| 이다.
위의 식을 자세히 살펴 보면, 정사영(projection)의 식과 동일한 것을 알 수 있다.
따라서 내적은 정사영이라는 것을 알 수 있다. 그러므로 내적을 통해 두 벡터 간의 닮은 정도를 알 수 있다.
그러면 내적의 크기가 가장 클까? 정답은 바로 두 벡터의 방향이 일치할 때이다. 즉, 두 벡터의 방향이 일치한다면 두 벡터의 내적 값이 가장 크며 제일 닮았을 때이다. 반대로 내적의 크기가 가장 작으려면 cosθ=0일 때(θ=90), 두 벡터가 수직일 때라는 것까지 알 수 있다.
 
예를 들어, 식육점 사장님이 되었다고 가정하고, 하루 동안 돼지고기, 소고기, 양고기의 판매량이 각각 (10, 6, 2)라고 하자. 그리고 각각의 가격이 (30000, 70000, 50000)이라고 하자. 그렇다면 하루 동안의 매출은 얼마일까?

하루 동안의 매출이 820,000원이 나왔다면 아래와 같은 계산을 한 것이다.
(30000, 70000, 50000) · (10, 6, 2) = 30000 * 10 + 70000 * 6 + 50000 * 2 
 
따라서 a바와 b바의 내적이 a바·b바로 표시되게 하면 아래와 같다.

출처: http://hyperphysics.phy-astr.gsu.edu/hbase/vsca.html

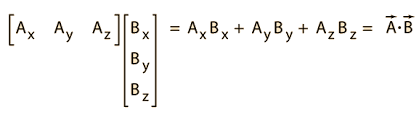
위와 같이 내적을 구할 때는 두 개의 벡터의 요소 수가 같아야 한다. 그리고 내적의 결과는 벡터가 아니라 스칼라(scalar)이다.
따라서 벡터의 내적(inner product)는 스칼라 곱(sclar product)라고도 하며 필자가 표현하는 것과 같이 dot product라고도 한다.
그리고 한 가지 주의해야 할 것이 있는데, 내적을 표현할 때는 a바xb바 또는 a바b바라고는 절대로 적지 않는다. 그 이유는 외적(outer product)를 표현할 때 사용하기 때문이다. 또한 영벡터가 아닌 두 벡터의 내적이 0이라면 두 벡터는 서로 직교(orthogonal)한다고 말하며 'a바⊥b바'라고 표현한다.
 
파이썬 실습
내적은 NumPy의 dot() 함수로 간단하게 구할 수 있으며 또한 sum() 함수를 사용해서 각 요소의 곱의 총합으로도 구할 수 있다.

dot() 함수, 곱의 총합 모두 같은 결과가 나오며, 내적은 두 개 벡터의 상관관계를 구할 때 등에 사용한다.
 

노름(norm)

노름은 '벡터의 크기'를 나타내는 양으로 인공지능(AI)에서 자주 쓰이는 놈으로는 'L² 노름'과 'L¹ 노름'이 있다.
놈은 인공지능에서 가중치 규제(regularization)에 쓰이는데 규제란 필요 이상으로 네트워크 학습이 진행되는 것을 파라미터를 조절해서 예방하는 것을 뜻한다.

출처: https://towardsdatascience.com/visualizing-regularization-and-the-l1-and-l2-norms-d962aa769932

L² 노름 - default

L2 노름은 위 식과 같이 벡터의 제곱합의 제곱근으로 정의된다.(피타고라스의 정리와 똑같다.)
L2 노름을 최소화하는 벡터를 찾는 L2 정규화는 선형 회귀(linear regression), 로지스틱 회귀(logistic regression), 인공신경망 모델 등에서 흔히 사용된다.
L2 정규화는 모델의 가중치(weight)를 제한함으로써 과대적합(overfitting)을 방지하고 모델의 일반화 성능을 향상시키는 효과를 가진다.
또한, L2 노름을 이용한 가중치 감소(weight decay) 방법은 인공신경망에서 매우 흔히 사용되는 방법 중 하나이다.
 

L¹ 노름

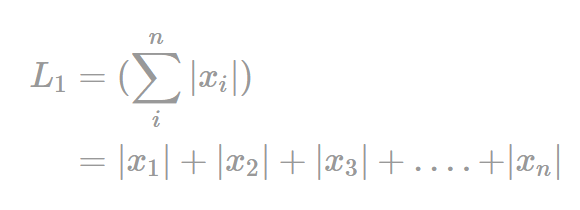
L1 노름은 벡터의 절댓값 합으로 정의되며, 이를 최소화하는 벡터를 찾는 L1 정규화(regularization)는 인공신경망 모델에서 흔히 사용된다. 그리고 L2 노름과 마찬가지로 모델의 과대적합(overfitting)을 방지하고 모델의 일반화 성능을 향상시키기 위해 사용된다.
 
일반화된 놈

 

출처: https://www.youtube.com/watch?v=NKuLYRui-NU

 
파이썬 실습
놈(norm)은 NumPy의 linalg.norm() 함수를 이용해 구할 수 있다. (*linalg: linear algebra)

노름의 종류에 따라 벡터의 크기는 다른 값이 됨을 확인할 수 있다.