[Linear Algebra] 행렬의 기초 with Python

행렬 - Matrix

기본 용어

행렬(matrix): 수나 문자를 직사각형 형태로 나타낸 것, 행렬의 크기는 행수 x 열수

행(row): 행렬의 가로줄 → m

열(column): 행렬의 세로줄 → n

→ 즉 (m, n의 성분을 주로 aₘₙ과 같이 나타냄)

주대각선(main diagona): 행렬의 왼쪽 위에서 오른쪽 아래를 가르는 선

→ 모든 행렬은 그 행렬의 성분 값에 상관없이 주 대각선을 갖는다.

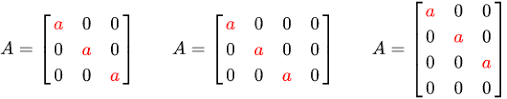
n차 행렬, n차 정방행렬:만약 행과 열의 수가 똑같은 N x N 형태의 행렬

ex 1. 행렬의 크기가 2x3인 행렬

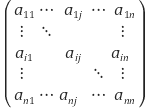
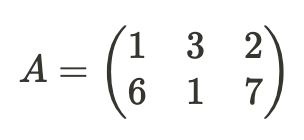
→ (1, 2)의 성분=3, (2,3)의 성분=7

 

ex 2. 행렬의 크기가 2x2인 행렬(2차 정방행렬)

→ (2, 1)의 성분=-1, (2, 2)의 성분=1

 

전치행렬(transposed matrix)

전치행렬: 각 행을 열로 바꾼 행렬 A → Aᵀ

 

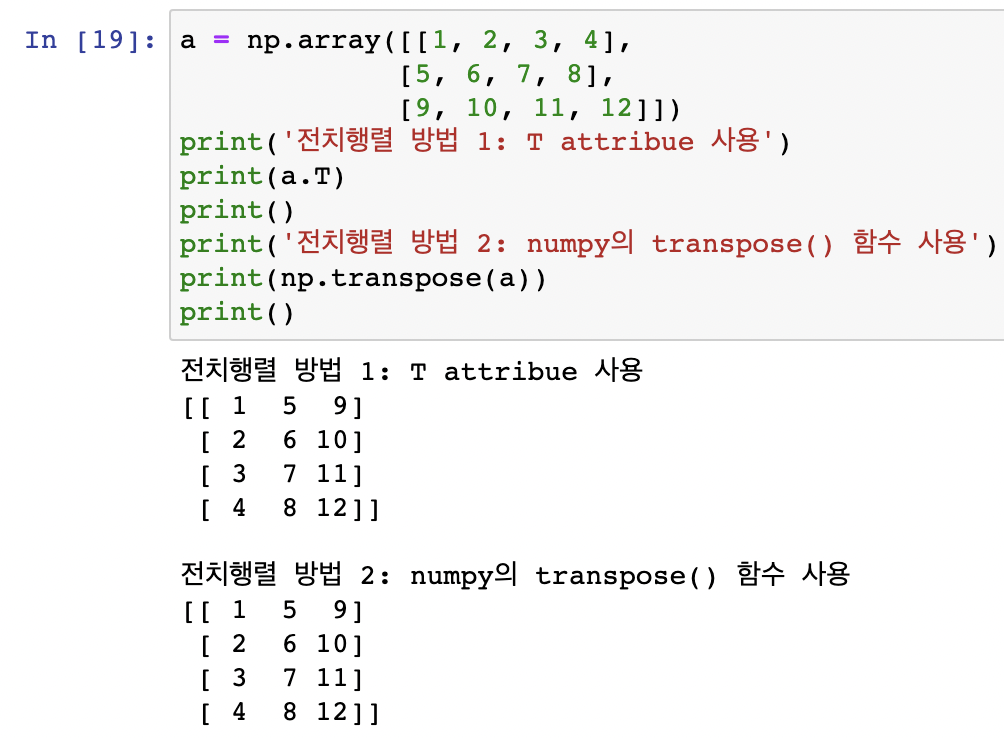
대칭행렬(symmetric matrix)

대칭행렬: 대칭행렬이 자기 자신과 같은 행렬

→ A는 대칭행렬 ↔ Aᵀ=A

대칭행렬의 특징

• 항상 행렬의 형태는 정사각형의 형태여야 함
• 대각성분에 대해 대칭적으로 생긴 행렬

출처: https://en.wikipedia.org/wiki/Symmetric_matrix

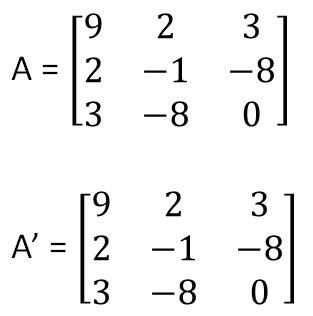
증명

 

대각행렬(diagonal matrix)

대각행렬: 대각성분이 아닌 모든 성분이 0인 행렬

→ 대각성분은 0이어도 됨

→ 대각성분에 대해서 대칭으로 생겼으므로 대칭행렬임

단위행렬(unit matrix, identity matrix: I) → 매우 중요

단위행렬: 대각성분들만 전부 1이고 나머지는 0인 행렬

→ 단위행렬 I는 정수에서 1과 같은 역할이므로 매우 중요함!

 

영행렬(zero matrix, null matrix: O)

영행렬: 모든 성분이 0인 행렬

 

A=B (Equality of matrix)

→ a=5, b=3, c=-1, d=1

 

행렬의 실수배, 덧셈, 뺄셈 ← 같은 크기의 행렬끼리만 연산 가능!

행렬의 실수배: 모든 성분에 각각 실수배만큼 곱해줌

Python의 NumPy로 실습

행렬의 덧셈과 뺄셈: 같은 위치에 있는 성분들끼리 더하거나 뺌

Python의 NumPy로 실습

 

학습 자료 다운로드

Learning Matrix.ipynb

0.00MB