자료의 위치점(position point)
어느 자료의 p% 위치점(position point)이:자료를 오름차순으로 나열하였을 때 전체 측정값 중에서 주어진 비율 p만큼의 측정값들이 그 값보다 작거나 같고 (1-p) 비율만큼의 측정값들이 그 값과 같거나 큰 값으로 정의된다.
- 전형적인 예는 중앙값이며, 백분위수(percentiles), 십분위수(deciles), 사분위수(quartiles)가 있다.
예를 통해 살펴보면, 아래와 같다.
- 자료의 분포에서 50%(p=0.5)가 중앙값과 같거나 작고 나머지 50%가 중앙값과 같거나 크다. 그러므로 중앙값은 50% 위치점이다.
백분위수(percentiles)
백분위수: n% 백분위수 pₙ은 측정값들을 작은 것부터 크기 순서로 나열하였을 때 적어도 n%의 측정값들이 pₙ과 같거나 작고, (100-n)%의 관측값들이 pₙ과 같거나 큰 값이 되도록 하는 값
글로만 보면 잘 와닫지 않으니, 아래의 예를 통해 살펴보자
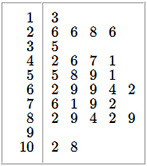
위 그림은 줄기-잎 그림(stem-and-leaf diagram)이다.
이를 오름차순으로 정렬한 배열로 바꿔보면, 아래와 같다.
[13, 26, 26, 26, 28, 35, 41, 42, 46, 47, 51, 55, 58, 59, 62, 62, 64, 69, 69, 71, 72, 76, 79, 82, 82, 84, 89, 89, 102, 108]
1. 이때, 25 백분위수인 p₂₅를 구해보면,
먼저 표본의 크기는 30이다.
p₂₅는 측정값들을 작은 것부터 순서대로 나열하였을 때 30*0.25(25%)=8(7.5에서 반올림)이므로, 42이다.
2. 30 백분위수를 찾으면 30*0.3=9, 9번째에 배열되는 수와 10번째에 배열되는 수의 평균값인 (46+47)/2=46.5이므로, p₃₀=46.5가 된다.
이를 통해, 편하게 구하는 방법을 알 수 있다. 자료의 개수가 n이고 비율이 p일 때,
1) n*p를 곱한 값이 자연수라면 n*p번째에 배열되는 수와 ((n*p) + 1)번째에 위치되는 수의 평균값을 구해주고
2) n*p를 곱한 값이 자연수가 아닐 경우 n*p의 수를 반올림해준 수에 해당하는 배열의 위치에 있는 수로 구할 수 있다.
사분위수(quartiles)
자료의 분포에는 3개의 사분위수(quartile)가 있다.
- 제1사분위수(Q₁), 제2사분위수(Q₂), 제3사분위수(Q₃)
사분위수는 자료의 측정값들을 오름차순으로 나열한 것을 25%씩 4등분하는 위치점들이며 아래와 같은 관계가 있다.
- Q₁ = p₂₅ (25 백분위수)
- Q₂ = x~ (중앙값) = p₅₀ (50 백분위수)
- Q₃ = p₇₅ (75 백분위수)
십분위수(deciles)
십분위수는 자료의 측정값을 오름차순으로 나열한 것을 10등분하는 위치점들이다. 따라서 9개가 있으며 아래와 같이 구분된다.
- 제1십분위수(D₁), 제2십분위수(D₂), ..., 제9십분위수(D₉)
그리고, 십분위수와 백분위수의 관계는 D₁ = P₁₀, D₂ = p₂₀, ..., D₉ = p₉₀이 성립된다.
십분위수 또한 예를 통해 알아보자.
아래의 데이터는 헬스를 즐겨하는 12명을 대상으로 데드리프트 무게(kg)를 조사했다고 가정하자.
| 80 | 89 | 100 | 105 | 120 | 125 |
| 127 | 140 | 145 | 156 | 180 | 190 |
1) 제1사분위수를 구하면?
Q₁ = p₂₅이므로, 25 백분위수를 구하면 빠르게 구할 수 있다.
12*0.25=3이 자연수이므로 오름차순으로 정렬된 배열의 3번째와 4번째에 위치한 수의 평균을 구해주면 된다.
따라서, (100+105)/2 = 102.5가 제1사분위수가 된다.
Q₁ = 102.5
2) 제2십분위수를 구하면?
D₂ = p₂₀이므로, 20 백분위수를 구하면 빠르게 구할 수 있다.
12*0.2=2.4인데 이는 자연수가 아니므로 반올림하여 3에 해당하는 위치한 수가 제2십분위수가 된다.
따라서, D₂ = 100
'Mathematics > Statistics' 카테고리의 다른 글
| [Statistics] 기술통계: 일변량 자료의 분석 - 왜도(비대칭도)와 첨도(꼬리부분의 두꺼움 정도) (0) | 2023.05.27 |
|---|---|
| [Statistics] 기술통계: 일변량 자료의 분석 - 산포도를 나타내는 통계값 (0) | 2023.05.26 |
| [Probability] 조합(Combinations) (0) | 2023.05.18 |
| [Statistics] 기술통계: 일변량 자료의 분석 - 대푯값 (0) | 2023.05.05 |
| [Statistics] 자료의 요약 (0) | 2023.04.30 |
