[Statistics] 자료의 요약

자료의 요약(summary of data)

통계학에서 가장 기본이 되는 단계: 자료 수집 단계 → 수집된 자료는 목적에 따라 분류되고 정리되어 분석됨

자료의 종류와 척도

자료의 종류

자료를 정리하는 방법은 분석의 대상이 되는 자료의 형태에 따라 달라짐

질적 자료(qualitative data)	관측된 결과가 숫자가 아닌 범주나 속성으로 분류되는 자료 → 범주형 자료(categorical data)라고도 함 ex) 성별(남, 여), 혈액형(A, B, O, AB), 출생지(부산, 서울, 인천, 제주도 등), etc.
양적 자료(quantitative data)	관측결과가 숫자로 표현되는 수치적 자료 → 관측되는 값의 성질에 따라 연속형과 이산형으로 나뉨 ex) 무게, 연령, 길이, 성적, etc. 연속형: 관측값이 셀 수 있는 값 → ex) 저금통 속의 동전수, 가족 내의 어린이 수, 개인의 봉급 등 이산형: 관측값이 구간에서의 자료 → ex) 자동차의 속도, 무게, 시간 등

주의할 점: 질적 자료와 양적 자료를 구분하는 것이 단지 자료가 숫자로 표현되는가의 여부에 따라 구분되는 것은 아님
→ 찬성은 1, 반대는 0으로 찬·반을 나타낸다면 이는 질적 자료로서 범주를 나타냄

자료의 척도

명목척도(nominal scale)	분류적인 의미, 둘 이상의 범주(category)로 구분되는 자료를 측정할 때 사용하는 척도 통계분석의 편의를 위해 숫자로 나타내기도 함(남:0, 여:1) 명목척도에 의해 측정된 자료는 사칙연산 의한 분석을 할 수 없고, 빈도를 분석 ex) 주민등록번호, 차번호, 남(0), 여(1) 등
순위척도(ordinal scale)	어느 사항의 정도에 따라 범주화하여 그 정도의 순서대로 배열한 것으로 범주 간의 상대적 순위를 측정 *사항의 정도: 고객의 만족도나 상품의 선호도 등 → 사회 및 여론조사의 설문에서 많이 사용되는 척도 순위척도에 의해 측정된 자료도 사칙연산에 의한 분석을 할 수 없고, 빈도를 분석 ex) · 성적 A, B, C, D, F · 조교수, 부교수, 교수 · 초등학교, 중학교, 고등학교, 대학교 등
구간척도(interval scale)	측정된 관측치 간의 차이가 양적으로 계산될 수 있도록 순위척도로 측정된 자료 절대 0점이 존재하지 않음 → 대표적인 예로 온도(절대적 0도의 개념이 없으므로 "몇 배로 덥다"는 해석은 옳지 않음) 구간척도에 의해 측정된 자료는 크기의 순서, 변수 간의 차에 대한 분석은 의미가 있으나, 비율(ratio)에 대한 분석은 의미가 없음, 평균과 분산이 의미 있음 ex) IQ 점수: 두 점수 차이는 계산되지만 IQ 180이 IQ 90의 두 배를 나타내는 것은 아님 온도: 0도는 온도가 없음을 뜻하는 것이 아님
비율척도(ratio scale)	구간척도가 갖는 특성에 0의 의미가 "없다"라는 뜻이 포함된 자료 → 비율계산이 가능한 일반적으로 사용되는 단위들 ex) 몸무게, 키, 혈압 등 대부분의 연속형 자료 → 사칙연산 가능, 평균과 분산이 의미가 있음

 

도수분포표를 이용한 자료의 정리

자료를 정리하는 목적은 전체자료의 형태를 파악하고 간단하게 분석하기 위해서임

정리하기 전의 자료를 원자료(raw data)라 하며, 원자료를 배열하는 하나의 방법은 자료를 크기순으로 정렬하는 것

하지만, 자료의 개수가 방대하면 크기순으로 배열하는 것은 다루기 어렵기 때문에 표를 이용해 원자료를 정리하는데 이 표를 '도수분포표(frequency table)'라 하며 도수는 동일한 측정값의 개수로서 질적 자료나 이산자료 정리에 이용되며 f로 표시함

https://allthingsstatistics.com/basics/frequency-distribution-table/

연속형 자료이거나 많은 관측값들로 구성되는 이산형 자료는 전체를 몇 개의 그룹으로 나누어 도수분포표를 만들면 됨

이때, 각 그룹을 계급(class)이라고 함 (ex: 위 사진에서 15~19, 20~24, ...)

계급의 개수를 정하는 것은 특별한 법칙이 있는 것은 아니며, 자료의 총수에 비해 너무 많거나 적은 개수의 계급을 사용하면 자료에 포함된 정보를 충분히 나타내지 못함

전체자료를 계급으로 나눌 때의 유의점

1) 각 계급은 동일한 간격(width)을 가져야 함

2) 어느 두 계급도 겹쳐져서는 안 됨

3) 모든 자료는 반드시 어느 하나의 계급에 속해야 함

상대 도수분포표(relative frequency table)

상대도수: P(A)

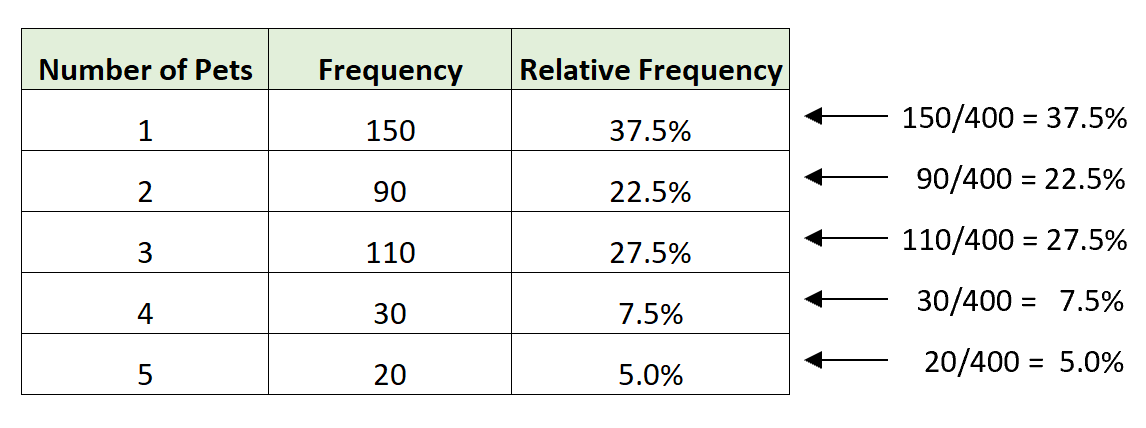
상대도수: 도수분포표에서 각 계급의 도수를 전체 관측자료 총수에 대한 비율

상대 도수분포표: 상대도수를 포함한 도수분포표

https://www.statology.org/relative-frequency-distribution/

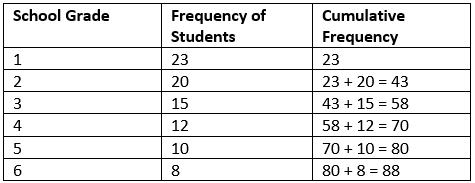
누적 도수분포표(cumulative frequency table)

누적도수: 각 계급의 도수를 계속 쌓아가는 것

누적 도수분포표: 누적도수를 포함하는 도수분포표

https://statisticsbyjim.com/basics/cumulative-frequency/

 

그래프를 이용한 자료의 정리

막대그래프와 원그래프

주로 범주형 자료와 명목형 자료에 이용

원그래프

예산정보의 표현에서처럼 전체에 대한 각 부분들을 나타낼 때 많이 이용

https://www.youtube.com/watch?v=wCwYzEJyOk8

막대그래프

범주형 자료에서 수평축에서는 범주, 수직축에는 각 범주에 대응되는 막대의 높이나 도수의 크기에 비례하도록 그림

https://www.mathematics-monster.com/widgets/bar_chart_from_frequency_table.html

히스토그램

도수분포표에서의 막대그래프의 일종 → 범주형 자료에서도 이용 가능

히스토그램을 작성할 때에는 막대의 넓이가 도수에 비례되도록 하기 위해 막대의 폭을 일정하게 해야 함

https://medium.com/wicds/what-is-histogram-d9e1fe230ae7