산포도를 나타내는 통계값
일반적으로 이전 포스팅에서 학습한 대푯값(https://psleon.tistory.com/39)과 위치점(https://psleon.tistory.com/60)만으로는 측정된 자료의 분포가 가진 특징을 적절하게 설명할 수 없다.
아래의 예는 'A'와 'B' 두 사격선수가 각각 10발씩 쏘아 얻은 점수라고 가정하여 얻은 점수를 나타낸 것이다.
| 점수 | 1 | 2 | 3 | 4 | 5 | |
| 도수 | A | 2 | 3 | 4 | 1 | 2 |
| B | 0 | 0 | 5 | 4 | 1 | |
A의 합은 1*2 + 2*3 + 3*4 + 4*1 +5*2 = 34이고 B의 합은 3*5 + 4*4 + 5*1 = 36이다.
이때 A의 경우는 평균득점(x')은 3.4이고, B의 경우는 평균득점(x')가 3.6이다.
그러나 'A'와 'B'의 득점 패턴에는 현저한 차이가 있다. 이를 아래와 같이 파이썬의 matplotlib 라이브러리를 활용하여 막대그래프로 나타내어 확인해보자.

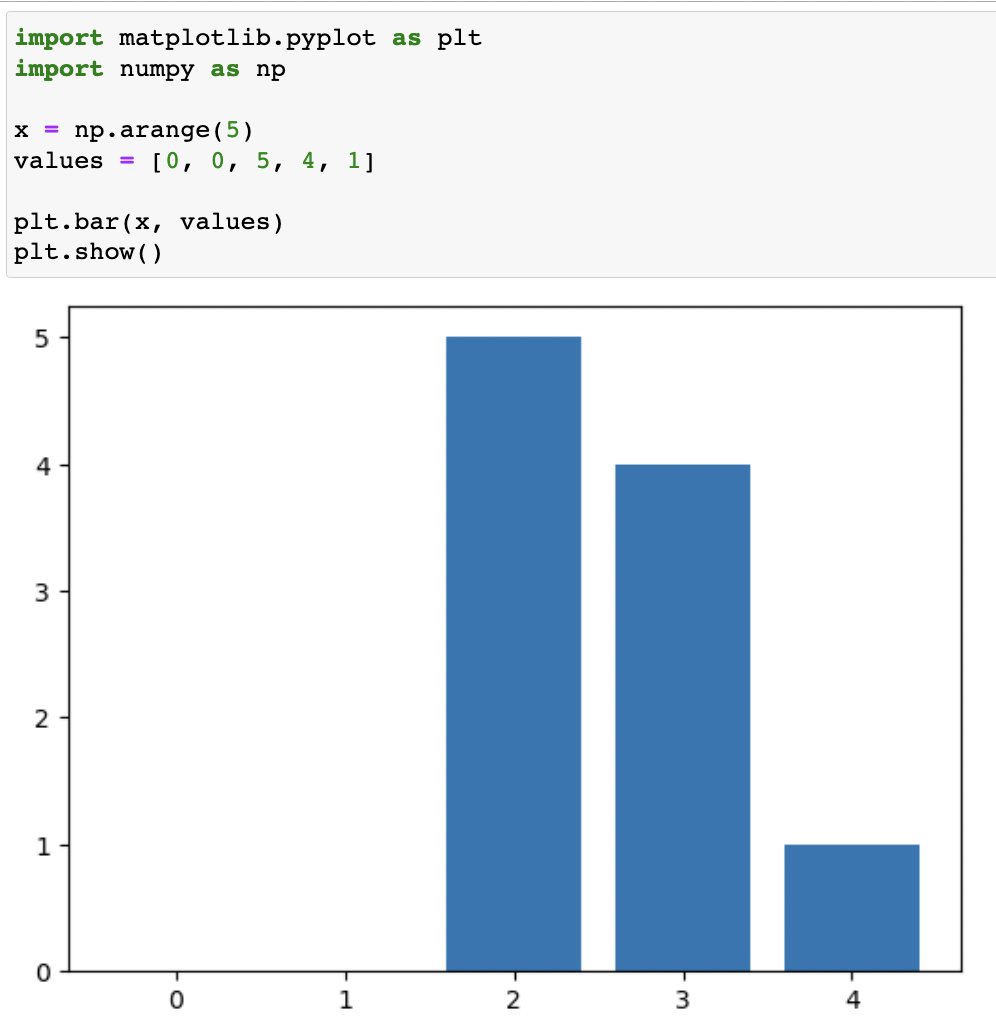
위 그래프를 살펴보면 'A'가 득점한 점수가 'B'의 점수보다 더 산포(dispersion)되어 있어 'A'의 변동성(variability)이 'B'보다 더 큼을 알 수 있다.
산포도
산포도(dispersion): 자료의 측정값들이 그 대푯값 주위에서 어느 정도 크기의 변동을 하며 분포되어 있는가를 계량하는 통계값
바로 직전 언급한 변동성(variability)은 통계학에서 매우 중요한 개념이기 때문에, 양적 자료의 변동성을 계량할 수 있는 산포도가 여러 종류 개발되어 있다, 그중에서도 특히 자주 사용되는 산포도인 범위(range), 사분위수 범위(interquartile range), 분산(variance)과 표준편차(standard deviation)에 대해 알아보고자 한다.
1) 범위(range)
자료의 측정값이 x1, x2, ..., xn일 때 범위 R은 = U(최댓값) - L(최솟값)으로 정의된다. 단, 최댓값과 최솟값은 1보다 크거나 같고 n보다 작거나 같다.
예제: 가족의 연령분포가 38, 6, 35, 4일 떄 범위 R은 38 - 4 = 34이다.
범위(range)는 계산이 간단해 가끔 계산이 복잡한 산포도를 간접적으로 추정하는 데도 사용되지만 유용하게 사용되는 산포도는 아니며 이상값에 크게 영향을 받는다.
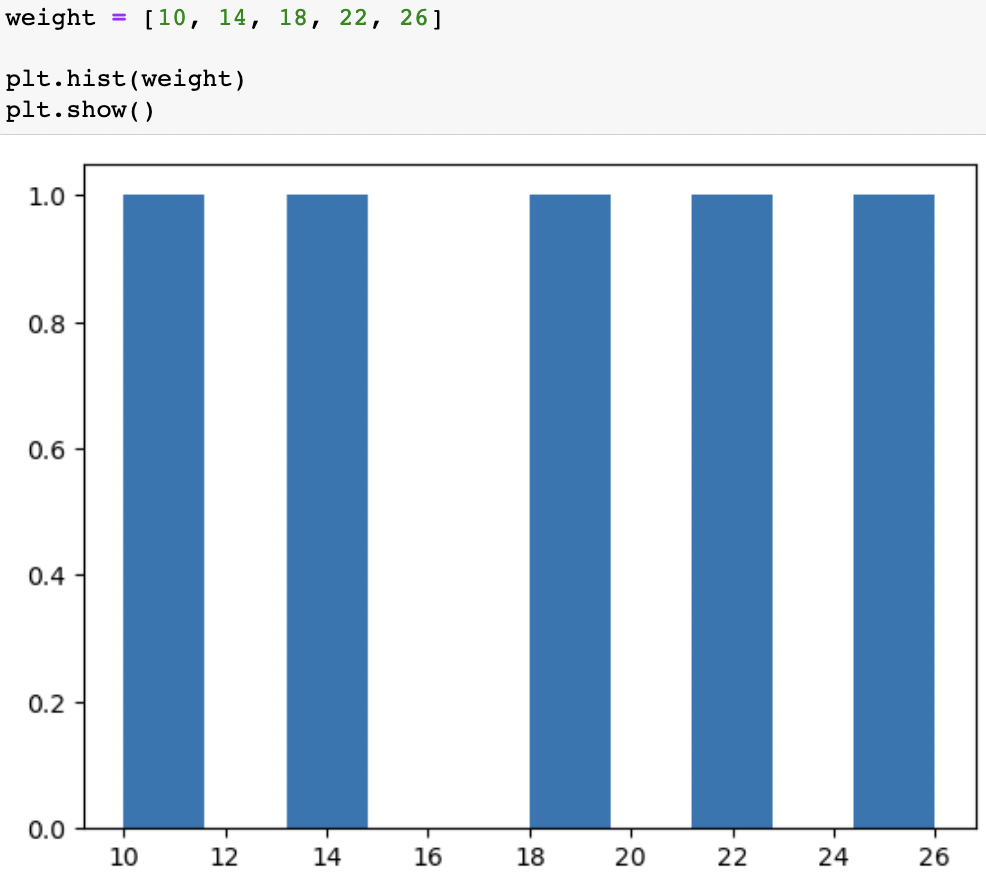
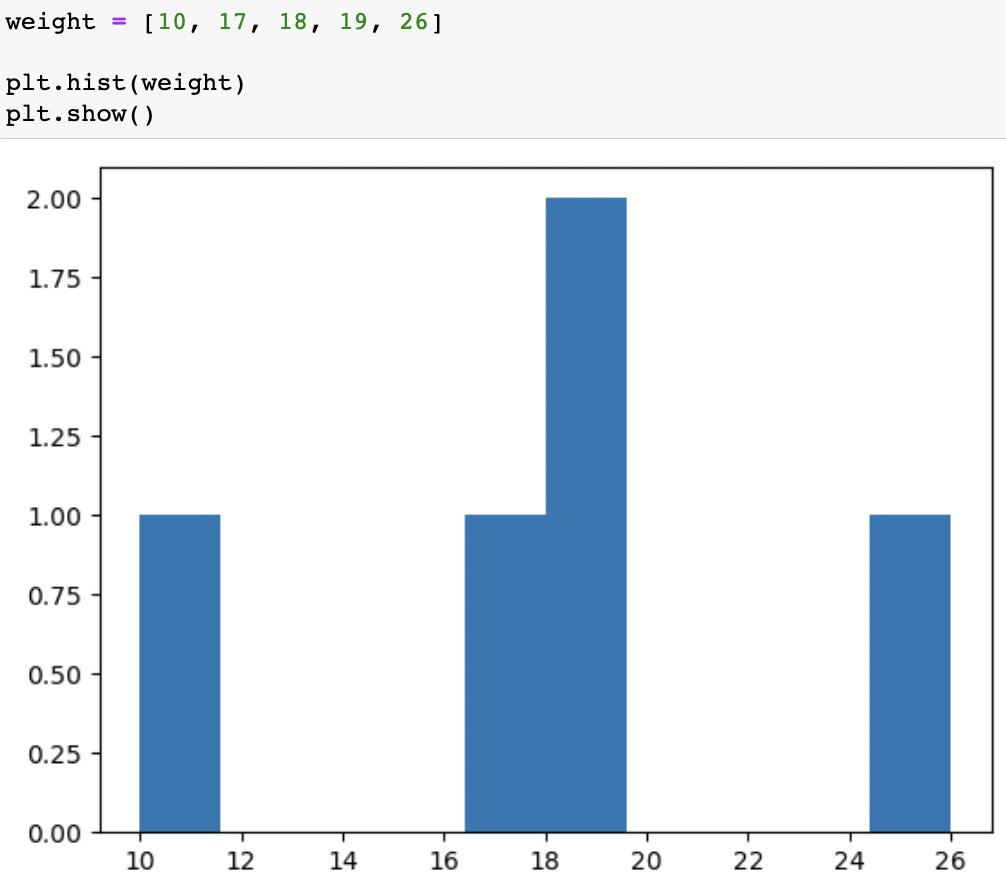
위 그림을 보면 두 자료의 범위는 R = 16으로 같다. 그러나 히스토그램을 보면 자료 A가 자료 B보다 더 산포되어 있다. 이를 통해 범위가 유용한 산포도가 아님을 확인할 수 있다.
2) 사분위수 범위(interquartile range)
자료의 제1사분위수를 Q1, 제3사분위수를 Q3라 할 때 사분위수 범위를 IQR로 나타내고 IQR = Q3 - Q1으로 정의된다.
앞서 살펴본 범위(range)는 자료에 포함된 이상값들의 영향을 받지만, 사분위수 범위(interquartile range)는 자료에 포함된 이상값들의 영향을 받지 않으며, 중앙값을 대푯값으로 사용할 때, 이에 대응하는 산포도로 사분위수 범위를 사용한다.
아래의 자료는 중년남성 21명을 대상으로 측정한 폐활량지수(ml/kg·g)이라고 가정했을 때, 이 자료의 사분위수 범위를 구하고자 한다.
| 12.81 | 14.95 | 15.83 | 15.97 | 17.90 | 18.27 | 18.34 | 19.82 | 19.94 | 20.62 |
| 20.88 | 20.93 | 20.99 | 21.15 | 22.16 | 22.24 | 23.16 | 23.56 | 24.01 | 35.78 |
| 36.73 |
Q1 = 0.25 * 21 = 6(5.25에서 반올림)번째에 위치한 data = 18.27이다.
같은 방법에 의하면 Q3 = 0.75 * 21 = 16(15.75 '')번째에 위치한 data = 22.24임을 알 수 있다. 따라서 IQR = Q3 - Q1 = 22.24 - 18.27 = 3.97이며 범위와는 달리 이상값인 35.78과 36.73에 영향을 받지 않음을 알 수 있다.
지금까지 학습한 범위와 사분위수 범위는 그 계산에 자료의 일부분만을 사용하고 있어 측정값들이 가진 산포에 대한 정보를 모두 반영하지 못한다. 즉 범위의 계산에는 측정값들의 최댓값과 최솟값만 필요하며, 사분위수 범위의 계산에는 Q1보다 작고 Q3보다 큰 측정값들의 정보는 제외된다. 따라서 자료에 있는 측정값들을 모두 사용하여 계산하여 이상값이 없는 경우, 범위와 사분위수 범위보다 더 정확한 산포도로 평가받고 있는 분산(variance)과 표준편차(standard deviation)을 알아보자.
3) 분산과 표준편차(variance and standard deviation)
분산과 표준편차는 자료의 측정값들이 평균을 중심으로 어느 정도 흩어져 분포하고 있는지를 측정하는 통계값이다.

측정값들이 x1, x2, ..., xN인 유한 모집단의 자료(population data)와 측정값들이 x1, x2, ..., xn인 표본 자료(sample data)의 분산(variance)과 표준편차는 각각 위와 같이 정의된다.
여기서 모분산(population variance)은 "시그마 제곱"으로 읽으며 표본분산(sample variance)은 "에스 제곱"으로 읽으며, 모표준편차(σ)는 "시그마", 표본표준편차(s)는 "에스"로 읽는다. 즉, 모집단의 자료와 표본자료의 분산과 표준편차는 서로 구분된다.
분산의 계산에 필요한 용어들은 아래와 같다.
- 편차점수(deviation score): i번째 관측값 xi와 평균의 차인 xi-x'값
- 제곱합(sum of squares): 모든 관측값들의 편차점수의 제곱합
| 예제 1 A 고등학교에서 표본으로 추출한 학생 5명의 수학점수는 30, 55, 60, 90, 100이었다. 이 자료의 분산과 표준편차 구하면? |
| 표본평균(x') = (30 + 55 + 60 + 90 + 100)/5 = 67 제곱합 = (30-67)^2 + (55-67)^2 + (60-67)^2 + (90-67)^2 + (100-67)^2 = 3180 따라서 분산(x^2) = 제곱합/(n-1) = 3180 / 4 = 795 표준편차는 분산을 제곱근해주면 되므로 795^(1/2) = 28.195744... |
| 예제 2 A 고등학교의 학생 5명의 수학점수는 30, 55, 60, 90, 100일 때 이 자료가 모집단의 자료인 경우, 이 자료의 분산과 표준편차 구하면? |
| 본 문제의 경우 표본집단이 아닌 모집단의 data이므로 분산의 경우 σ^2 = 3180, 표준편차의 경우 σ = 28.195744...가 된다. |
위의 예제 1을보면 분산을 구했을 때, 원래 단위의 제곱형태이므로 값이 커져 분산 값을 해석하는 데 어려움이 있다. 따라서 원래 자료를 단위로 나타낼 수 있는 분산의 데이터에 양의 제곱근을 사용한 산포도가 제안되었는데 이것이 바로 표준편차(standard deviation)이다.
참고로 1)에서 학습한 자료의 범위(R)를 이용하면 표본표준편차(s)의 근사값을 간단히 계산할 수 있다.
s ≈ R/4
| 예제 3 어떤 표본 자료의 최댓값은 90이고 최솟값은 30이다. 또한, 이 자료로부터 계산된 표준편차는 185였다. s의 계산 결과를 믿을 수 있는가? |
| 범위(R)을 구해보면 90 - 30 = 60이고, s의 추정값 ≈ 60/4 = 15이다. 그러나 계산된 표준편차는 185이므로 차이가 너무 크기때문에 s의 계산에 오류가 있을 가능성이 크다고 볼 수 있다. |
주의할점은 분산과 표준편차는 이상값(outliers)들의 영향을 많이 받는 산포도라는 것을 염두에 두고 사용해야 한다는 것이다.
만약, 자료에 이상값이 포함되어 있으면 분산과 표준편차 대신 사분위수 범위를 산포도로 사용하는 것이 바람직하다.
'Mathematics > Statistics' 카테고리의 다른 글
| [Statistics] 기술통계: 일변량 자료의 분석 - 표준점수 (0) | 2023.05.27 |
|---|---|
| [Statistics] 기술통계: 일변량 자료의 분석 - 왜도(비대칭도)와 첨도(꼬리부분의 두꺼움 정도) (0) | 2023.05.27 |
| [Statistics] 기술통계: 일변량 자료의 분석 - 자료의 위치점 (0) | 2023.05.23 |
| [Probability] 조합(Combinations) (0) | 2023.05.18 |
| [Statistics] 기술통계: 일변량 자료의 분석 - 대푯값 (0) | 2023.05.05 |
