[Mathematics] 함수(Function)

함수(Function)

집합 X의 각 원소 x에 집합 Y의 원소 y가 오직 하나만 대응하는 규칙을 X에서 Y로의 함수(function from X into Y) 또는 사상(mapping)이라 하고, 기호로 f : X → Y로 나타낸다. 그리고 함수는 보통 문자로 f, g, h로 표현한다. 가장 중요한 것은 하나의 x에는 반드시 하나의 y만 대응해야 한다는 것이다. 

 

https://www.onlinemath4all.com/identifying-functions-from-mapping-diagrams.html

위의 경우는 함수가 아니다. 왜냐하면 집합 Input의 원소가 집합 Output의 원소로 mapping 할 때, 원소 2가 20과 40에 mapping 하는데 오직 하나만 대응하는 규칙을 어긴 것이므로 함수라 할 수 없다.

https://slideplayer.com/slide/1407079/

이 때, 집합 X를 함수 f의 정의역(domain), 집합 Y를 함수 f의 공역(codomain)이라 한다. 한 함수 y = f(x)의 정의역과 공역은 함수값 f(x)가 정의될 수 있는 실수의 집합에서 생각하기로 하고, 정의역을 집합 {x|a≤x≤b}와 같이 표기할 경우에는 다음과 같이 나타낼 수 있다.

y = f(x) (a≤x≤b)

 

함수 f : X → Y에서 X의 원소 x에 대응하는 Y의 원소 y를 f(x)로 나타내고, 이 f(x)를 f에 의한 x의 함숫값(value of function)이라 하며 y = f(x)와 같이 나타낸다.

그리고 함수 f : X → Y에서 함수값 전체의 집합

f(x) = {y | y = f(x), x ∈ X}

를 함수 f의 치역(range)이라 한다. 이 때, 치역은 공역의 부분집합임을 알 수 있다.

마지막으로 x를 독립변수(independent variable), y를 종속변수(dependent variable)라 한다.

 

정의로만 살펴보면 쉽게 이해하기 어려우니 간단한 예제를 통해 확인해보자.

https://www.geeksforgeeks.org/total-number-possible-functions/

위 그림에서 왼쪽이 집합 X, 오른쪽이 집합 Y로 가정하고 대응관계를 보고 함수인지 그리고 함수라면 함수값, 정의역, 공역, 치역을 하나씩 살펴보자.

 

먼저 집합 X의 각 원소에 Y의 원소 하나씩만 대응하고 있으므로 이 대응은 함수이다.

그리고 함수값을 살펴보면 f(a) = f(b) = f(c) = 4이다.

f의 정의역은 X = {a, b, c}

f의 공역은 Y = {4, 5}

f의 치역은 {4}이다.

 

정의역, 공역, 치역을 간단히 다시 정의하자면 정의역은 X의 범위, 공역은 Y의 범위, 치역은 Y 중에서도 함수값의 범위라고 할 수 있다.

 

다음으로 일대일함수, 전사함수, 일대일대응함수, 항등함수를 알아보자.

 

일대일함수(one-to-one function)

일대일함수(one-to-one function)는 단사함수(injective function)라고도 하며 집합 X의 원소가 집합 Y의 원소에 mapping 할 때 서로 다른 값에 mapping 되는 것, 즉 함수값이 한 곳이 아니라 다 다른 경우가 일대일함수이다.

위에서 살펴본 예시를 다시 보면 전부 4에 mapping 하는 것을 확인할 수 있는데 이 경우 일대일함수가 아니다.

 

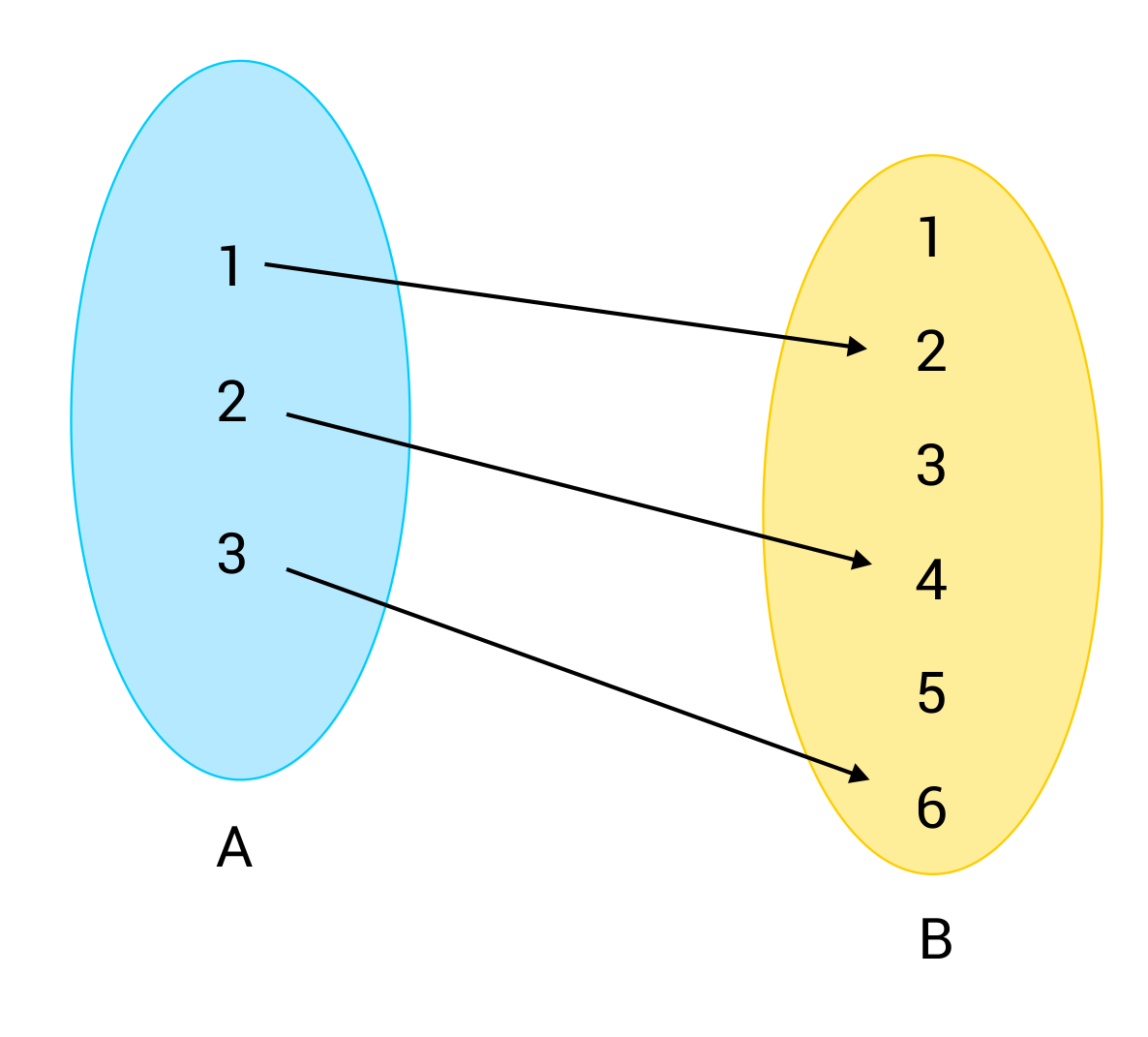
만약 위와 같은 경우에는 정의역에 해당하는 원소값이 모두 다른 값을 mapping 하기 때문에 일대일함수라고 할 수 있다.

 

전사함수(surjective function)

전사함수(surjective function)은 공역과 치역이 일치할 때, 즉 공역에 있는 모든 원소값이 함수값이 되는 경우를 뜻한다.

예시를 통해 살펴보자.

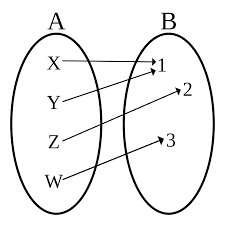
위 그림에서 공역은 B = {1, 2, 3}이다. 그리고 치역도 {1, 2, 3}이다. 따라서 전사함수라 할 수 있다.

 

일대일대응함수(bijective function)

일대일대응함수(bijective function)은 전단사함수라고도 하며, 일대일함수면서 전사함수일 때를 뜻한다.

예시를 보면 쉽게 이해할 수 있다.

https://j1w2k3.tistory.com/706

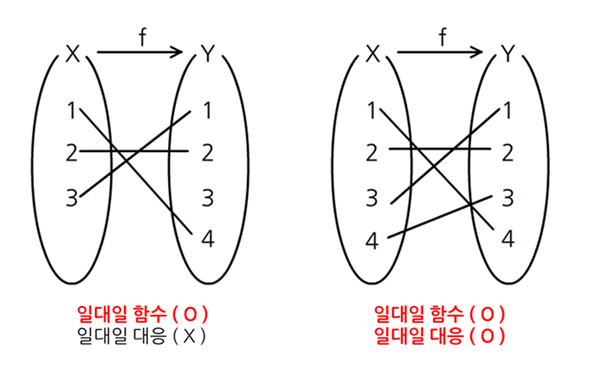
위 그림을 보면 왼쪽의 경우 일대일함수는 맞지만 일대일대응함수는 아니다. 그리고 오른쪽의 경우 일대일함수이면서 일대일대응함수이다.

왼쪽의 경우, 일대일 대응이 아닌 이유는 공역에 있는 3이 mapping이 되지 않았으므로 전사함수가 아니다. 그러나 정의역에 해당하는 원소 소값이 모두 다른 함수값을 mapping 하기 때문에 일대일 함수는 맞다.

오른쪽의 경우, 공역과 치역이 일치하므로 전사함수이다. 그리고 모두 다른 함수값을 mapping 하기 때문에 일대일 함수이다. 일대일함수이면서 전사함수라는 조건을 충족하므로 일대일 대응한다고 할 수 있다.

 

항등함수(identity function)

정의역 X의 임의의 원소 x에 그 자신이 대응하는 함수 f가 f(x) = x일 때 f를 항등함수(identity function)라 한다.

즉 f(1) = 1, f(2) = 2, f(3) = 3, ... 와 같이 자기 자신이 함수값인 형태가 바로 항등함수이다. 내용이 쉬우므로 예시 이미지만 첨부하고 설명은 생략하도록 한다.

 

 

합성함수(composite function)

두 함수

 f : X → Y,

 g : Y → Z

가 있다.

이때 f에 의해 x∈X가 f(x)∈Y에 대응하고 g에 의해 f(x)∈Y가 g(fx))∈Z에 대응한다면 X를 정의역, Z를 공역으로 하는 새 함수를 정의할 수 있다.

이 함수를 f와 g의 합성함수(composite function)라 하고

g∘f : X → Z

로 나타내며 합성함수 g∘f는 y = g(f(x))로 나타낸다.

* 일반적으로 두 함수 g와 f의 합성함수는 교환법칙이 성립하지 않는다. 즉, g(f(x)) ≠ f(g(x))

https://byjus.com/maths/composition-of-functions/

 

역함수(inverse function)

Y의 임의의 원소 y에 y = f(x)인 X의 원소 x를 대응시키는 새 함수, 정의역이 Y이고 공역이 X인 새함수를 정의할 수 있는데 이때의 함수를 f : X → Y의 역함수(inverse function)라 한다. 즉 x와 y를 서로 바꾸는 것이다.

https://en.wikipedia.org/wiki/Inverse_function

 

*함수와 역함수를 합성하면 항등함수가 된다.